【題目】已知底面邊長為a的正三棱柱
（底面是等邊三角形的直三棱柱）的六個(gè)頂點(diǎn)在球
上，且球
與此正三棱柱的5個(gè)面都相切，則球與球的表面積之比為________.
【答案】
【解析】
設(shè)球
與球
的半徑分別為R，r，由題意分析球的半徑等于正三棱柱底面正三角形內(nèi)切圓的半徑，且等于正三棱柱高的一半，求出其半徑r，再由球的球心在上下底面中心連線的中點(diǎn)上，求出半徑R，再由球的表面積公式求出比值即可.
設(shè)球與球的半徑分別為R，r，因?yàn)榍?/span>與此正三棱柱的5個(gè)面都相切，所以球的半徑等于正三棱柱底面正三角形內(nèi)切圓的半徑，且等于正三棱柱高的一半，如圖所示，因?yàn)檎庵?/span>
底面邊長為a的正三棱柱，所以
，所以
，
，因?yàn)檎庵?/span>的六個(gè)頂點(diǎn)在球上，所以球的球心在上下底面中心連線的中點(diǎn)上，所以
，所以球與球的表面積之比為
，所以表面積之比為.
故答案為：
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖1，在邊長為3的菱形
中，已知
，且
.將梯形
沿直線
折起，使
平面
，如圖2，
分別是
上的點(diǎn).
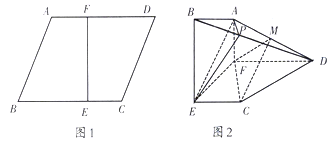
（1）若平面
平面
，求
的長；
（2）是否存在點(diǎn)
，使直線
與平面
所成的角是
？若存在，求出
的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)橢圓
的右焦點(diǎn)為
，過點(diǎn)作與
軸垂直的直線
交橢圓于
，
兩點(diǎn)（點(diǎn)在第一象限），過橢圓的左頂點(diǎn)和上頂點(diǎn)的直線
與直線交于
點(diǎn)，且滿足
，設(shè)
為坐標(biāo)原點(diǎn)，若
，
，則該橢圓的離心率為（ ）
A. 
B. 
C. 或 D. 
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
（
為常數(shù)）.
（1）求
的極值；
（2）設(shè)
，記
，已知
為函數(shù)
是兩個(gè)零點(diǎn)，求證： 
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在底面是正方形的四棱錐
中，
平面
，
，
是
的中點(diǎn).
（1）求證：
平面
；
（2）在線段
上是否存在點(diǎn)
，使得
平面？若存在，求出
的值；若不存在，說明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
的離心率為
，左、右焦點(diǎn)分別為
、
，
為橢圓C上一點(diǎn)，且
的中點(diǎn)B在y軸上，
.
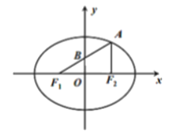
（1）求橢圓C的標(biāo)準(zhǔn)方程：
（2）若直線
交橢圓于P、Q兩點(diǎn)，若PQ的中點(diǎn)為N，O為原點(diǎn)，直線ON交直線
于點(diǎn)M，求
的最大值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】記數(shù)列
的前n項(xiàng)和為
，其中所有奇數(shù)項(xiàng)之和為
，所有偶數(shù)項(xiàng)之和為
若是等差數(shù)列，項(xiàng)數(shù)n為偶數(shù)，首項(xiàng)
，公差
，且
，求；
若數(shù)列的首項(xiàng)，滿足
，其中實(shí)常數(shù)
，且
，請寫出滿足上述條件常數(shù)t的兩個(gè)不同的值和它們所對應(yīng)的數(shù)列．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】[選修4—4：坐標(biāo)系與參數(shù)方程]
在直角坐標(biāo)系
中，曲線
的方程為
．以坐標(biāo)原點(diǎn)為極點(diǎn)，
軸正半軸為極軸建立極坐標(biāo)系，曲線
的極坐標(biāo)方程為
．
（1）求的直角坐標(biāo)方程；
（2）若與有且僅有三個(gè)公共點(diǎn)，求的方程．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】秦九韶是我國南宋時(shí)期的數(shù)學(xué)家，普州（現(xiàn)四川省安岳縣）人，他在所著的《數(shù)書九章》中提出的多項(xiàng)式求值的秦九韶算法，至今仍是比較先進(jìn)的算法．如圖所示的程序框圖給出了利用秦九韶算法求某多項(xiàng)式值的一個(gè)實(shí)例．若輸入n，x的值分別為5，2，則輸出v的值為( )
A. 64 B. 68
C. 72 D. 133
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com