Question

已知函數f（x）=|x|+

m

x

-1（x≠0）．
（1）若對任意x∈R，不等式f（2^x）＞0恒成立，求m的取值范圍；
（2）討論函數f（x）零點的個數．

Answer 1

考點：函數恒成立問題,函數零點的判定定理

專題：綜合題,函數的性質及應用

分析：（1）f（2^x）＞0恒成立?2^x+

m

2x

-1＞0（x≠0）恒成立?m＞2^x（1-2^x）（x≠0）恒成立，構造函數g（x）=2^x（1-2^x）（x≠0），利用基本不等式（或配方法）可求得m的取值范圍；
（2）當x＞0時，由f（x）=x+

m

x

-1=0得：m=x（1-x）=-（x-

1

2

）²+

1

4

；同理可得，當x＜0時，m=x（1+x）=（x+

1

2

）²-

1

4

，在在同一直角坐標系中作出函數y=m與函數y=|x|（x-1）的圖象，借助圖象即可求得函數f（x）零點的個數．

解答： 解：（1）f（2^x）＞0恒成立?2^x+

m

2x

-1＞0（x≠0）恒成立?m＞2^x（1-2^x）（x≠0）恒成立，
令g（x）=2^x（1-2^x）（x≠0），
則m＞g（x）_max，
因為g（x）=2^x（1-2^x）≤（

2x+(1-2x)

2

）²=

1

4

（當且僅當x=-1時取“=”），
∴g（x）_max=

1

4

，
∴m＞

1

4

；
（2）當x＞0時，由f（x）=x+

m

x

-1=0得：m=x（1-x）=-（x-

1

2

）²+

1

4

，
當x＜0時，由f（x）=-x+

m

x

-1=0得：m=x（1+x）=（x+

1

2

）²-

1

4

，
在同一直角坐標系中作出函數y=m與函數y=|x|（x-1）的圖象，

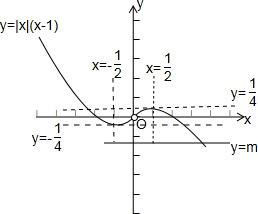
由圖象知，當m＜-

1

4

或m＞

1

4

時，函數f（x）=|x|+

m

x

-1（x≠0）有一個零點；
當m=±

1

4

或m=0時，函數f（x）=|x|+

m

x

-1（x≠0）有兩個零點；
當-

1

4

＜m＜0或0＜m＜

1

4

時，函數f（x）=|x|+

m

x

-1（x≠0）有三個零點．

點評：本題考查函數恒成立問題，考查函數零點的判定定理的應用，作圖是關鍵，也是難點，著重考查等價轉化思想與數形結合思想、分類討論思想的綜合運用，屬于難題．