【題目】受突如其來的新冠疫情的影響，全國各地學校都推遲2020年的春季開學.某學校“停課不停學”，利用云課平臺提供免費線上課程.該學校為了解學生對線上課程的滿意程度，隨機抽取了500名學生對該線上課程評分.其頻率分布直方圖如下：若根據頻率分布直方圖得到的評分低于80分的概率估計值為0.45.
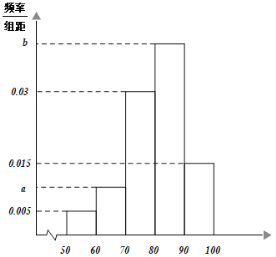
（1）（i）求直方圖中的a，b值；
（ii）若評分的平均值和眾數均不低于80分視為滿意，判斷該校學生對線上課程是否滿意？并說明理由（同一組中的數據用該組區間的中點值為代表）；
（2）若采用分層抽樣的方法，從樣本評分在[60，70）和[90，100]內的學生中共抽取5人進行測試來檢驗他們的網課學習效果，再從中選取2人進行跟蹤分析，求這2人中至少一人評分在[60，70）內的概率.
【答案】（1）（i）a＝0.01；b＝0.04（ii）該校學生對線上課程滿意，詳見解析（2）
【解析】
（1）
由頻率分布直方圖中小矩形面積之和為1，能求出
，
．
由頻率分布直方圖能求出評分的眾數和評分的平均值，從而得到該校學生對線上課程滿意．
（2）由題知評分在
，
和
，
內的頻率分別為0.1和0.15，則抽取的5人中，評分在，內的為2人，評分在，
的有3人，記評分在，內的3位學生為，，
，評分在，內的2位學生這
，
，從5人中任選2人，利用列舉法能求出這2人中至少一人評分在，的概率．
解：（1）由已知得
，
解得
，
又
，
．
由頻率分布直方圖得評分的眾數為85，
評分的平均值為
，
該校學生對線上課程滿意．
（2）由題知評分在，和，內的頻率分別為0.1和0.15，
則抽取的5人中，評分在，內的為2人，評分在，的有3人，
記評分在，內的3位學生為，，，
評分在，內的2位學生這，，
則從5人中任選2人的所有可能結果為：
，
，
，
，
，
，
，
，
，
，共10種，
其中，評分在，內的可能結果為，，，共3種，
這2人中至少一人評分在，的概率為
．
習題精選系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）＝xlnx，函數g（x）＝kx﹣cosx在點
處的切線平行于x軸.
（1）求函數f（x）的極值；
（2）討論函數F（x）＝g（x）﹣f（x）的零點的個數.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，焦距為
，直線
過橢圓的
左焦點.
（1）求橢圓的標準方程；
（2）若直線
與
軸交于點
是橢圓上的兩個動點,
的平分線在軸上,
.試判斷直線
是否過定點，若過定點，求出定點坐標;若不過定點，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）
|2x﹣3|，g（x）|2x+a+b|.
（1）解不等式f（x）
x2；
（2）當a
0，b0時，若F（x）f（x）+g（x）的值域為[5，+∞），求證：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，圓
上一點
處的切線
分別交
軸軸于點
，以為頂點且以
為中心的橢圓記作
，直線
交于
兩點.
（1）若橢圓的離心率為
，求
點坐標；
（2）證明：四邊形
的面積
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從某地區小學的期末考試中抽取部分學生的數學成績，由抽查結果得到如圖的頻率分布直方圖，分數落在區間
，
，
內的頻率之比為
．
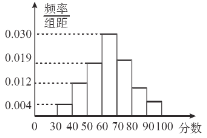
（1）求這些學生的分數落在區間內的頻率；
（2）若將頻率視為概率，從該地區小學的這些學生中隨機抽取3人，記這3人中成績位于區間
內的人數為
，求的分布列與數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若數列
滿足n≥2時，
，則稱數列
(n
)為的“L數列”．
（1）若
，且的“L數列”為
，求數列的通項公式；
（2）若
，且的“L數列”為遞增數列，求k的取值范圍；
（3）若
，其中p＞1，記的“L數列”的前n項和為
，試判斷是否存在等差數列
，對任意n，都有
成立，并證明你的結論．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在四棱錐P-ABCD中，底面ABCD為直角梯形，
，
，
，
，且平面
平面ABCD.
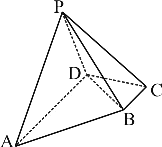
（1）求證：
；
（2）在線段PA上是否存在一點M，使二面角M-BC-D的大小為
？若存在，求出
的值；若不存在，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
