
如圖,正三棱柱![]() 的所有棱長都相等,D為
的所有棱長都相等,D為![]() 的中點.
的中點.
(1) 求證:平面![]()
(2) 求直線BD與平面![]() 所成的角
所成的角
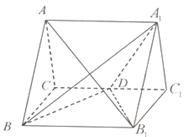
解:解法一:
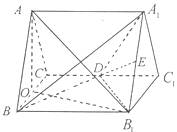
(1)取BC中點O,連結AO.
∵△ABC為正三角形, ∴AO⊥BC
正三棱柱ABC-A1B1C1中。平面ABC⊥平面BCClB1。,平面ABC∩平面BCC1B1=BC
∴AO⊥平面BC C1B1
連結B1O,在正方形BB1C1C中,O、D分別為BC、CC1的中點
∴BlO⊥BD
∴ABl⊥BD
在正方形ABB1A1中,AB1⊥A1B,
∴AB1⊥平面A1BD
(Ⅱ)設正三棱錐的棱長為2,在RtA1DC1中,A1C1=2,C1D=1
∴ A1D=![]() 同理B1D=BD=
同理B1D=BD=![]()
作DE⊥A1B1,則E為A1B1的中點,DE=2
∴![]()
由(I)AO⊥平面BCC1B1,且AO=![]()
∴A1到面BB1D的距離為![]() ,設點B到面A1B1D的距離為h,
,設點B到面A1B1D的距離為h,
由![]() 得
得![]()
∴![]()
設BD與平面A1B1D所成的角為0,
則![]()
因此,BD與平面A1B1D所成的角為![]()
解法二:

(Ⅰ)取BC中點O,連結AO.∵ △ABC為正三角形。∴OA⊥BC.
∵在正三棱柱ABC-A1B1C1中,平面ABC⊥平面BC1C1Bl,
∴ AO⊥平面BCC1B1.
取B1C1中點O1,以O為原點,![]() ,
,![]() ,
,![]() 的方向為x,y,z軸的正方向建立空間直角坐標系,
的方向為x,y,z軸的正方向建立空間直角坐標系,
設正三棱錐的棱長為2,則B(1,0,0),D(一1,1,0),A.(0,2,![]() ),A(0,0,
),A(0,0,![]() ),B.(1,2,0),
),B.(1,2,0),
∴![]() =(1,2,一
=(1,2,一![]() ),
),![]() =(-2,1,0),
=(-2,1,0),![]() =(一1,2,
=(一1,2,![]() ),
),
∵![]() ?
?![]() =-2+2+0 =0,
=-2+2+0 =0, ![]() ?
?![]() =-1+4 -3=0,
=-1+4 -3=0,
∴![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() ,∴AB1⊥平面A1BD.
,∴AB1⊥平面A1BD.
(Ⅱ)![]() =(1,1,
=(1,1,![]() ),
),![]() =(1,0,
=(1,0,![]() ).設平面A1B1D的法向量n=(x1,y1,z1).
).設平面A1B1D的法向量n=(x1,y1,z1).
則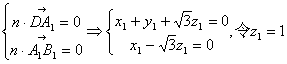 得
得
n=(![]() ,
,![]() ,1)為平面A1B1D的一個法向量.
,1)為平面A1B1D的一個法向量.
∵![]() ∴
∴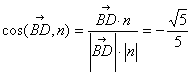
因此,BD與平面A1B1D所成的角為![]() 。
。


科目:高中數學 來源:河南省09-10學年高二下學期期末數學試題(理科) 題型:解答題
(本小題滿分13分)如圖,正三棱柱 的所有棱長都為2,
的所有棱長都為2, 為
為 的中點。
的中點。
(Ⅰ)求證: ∥平面
∥平面 ;
;
(Ⅱ)求異面直線 與
與 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

[來源:KS5
U.COM
查看答案和解析>>
科目:高中數學 來源:2007年普通高等學校招生全國統一考試理科數學卷(福建) 題型:解答題
(本小題滿分12分)
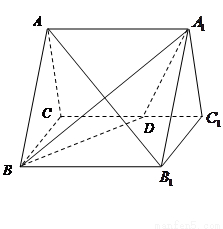 如圖,正三棱柱
如圖,正三棱柱 的所有棱長都為
的所有棱長都為
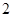 ,
,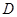 為
為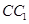 中點.
中點.
(Ⅰ)求證: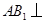 平面
平面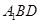 ;
;
(Ⅱ)求二面角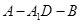 的大小;
的大小;
(Ⅲ)求點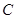 到平面
到平面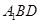 的距離.
的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com