
 的左、右焦點,P為橢圓C上任意一點,且
的左、右焦點,P為橢圓C上任意一點,且 最小值為0.
最小值為0.
 坐標關于x、y的形式,從而得到
坐標關于x、y的形式,從而得到 ,結合點P為橢圓C上的點,化簡得
,結合點P為橢圓C上的點,化簡得 ,說明
,說明 最小值為1-c2=0,從而解出a2=2且b2=1,得到橢圓C的方程.
最小值為1-c2=0,從而解出a2=2且b2=1,得到橢圓C的方程. ,
, -------------(1分)
-------------(1分)
 ,可得y2=
,可得y2= x2,
x2, -------------(2分)
-------------(2分) 最小值為1-c2=0,解之得c=1,可得a2=2,-------------------(3分)
最小值為1-c2=0,解之得c=1,可得a2=2,-------------------(3分) .---------------------------------------------(4分)
.---------------------------------------------(4分) ,即|k2t2-m2|=k2+1,---------------------------------(10分)
,即|k2t2-m2|=k2+1,---------------------------------(10分) 和
和 ,---------------------------(13分)
,---------------------------(13分) ;定點(1,0)到直線l1,l2的距離之積為
;定點(1,0)到直線l1,l2的距離之積為 ,也符合題意.
,也符合題意. 最小值為0的情況下求橢圓的方程,并討論x軸上存在定點B到l1,l2的距離之積恒為1的問題,著重考查了橢圓的標準方程與簡單幾何性質、點到直線的距離公式、向量數量積運算和直線與圓錐曲線的位置關系等知識點,屬于中檔題.
最小值為0的情況下求橢圓的方程,并討論x軸上存在定點B到l1,l2的距離之積恒為1的問題,著重考查了橢圓的標準方程與簡單幾何性質、點到直線的距離公式、向量數量積運算和直線與圓錐曲線的位置關系等知識點,屬于中檔題. 

 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
 (2013•揭陽一模)如圖,設點F1(-c,0)、F2(c,0)分別是橢圓C:
(2013•揭陽一模)如圖,設點F1(-c,0)、F2(c,0)分別是橢圓C:| x2 |
| a2 |
| PF1 |
| PF2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•揭陽一模)如圖,設點F1(-c,0)、F2(c,0)分別是橢圓C:
(2013•揭陽一模)如圖,設點F1(-c,0)、F2(c,0)分別是橢圓C:| x2 |
| a2 |
| PF1 |
| PF2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
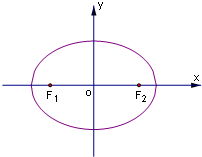 如圖,設點F1(-c,0)、F2(c,0)分別是橢圓
如圖,設點F1(-c,0)、F2(c,0)分別是橢圓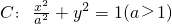 的左、右焦點,P為橢圓C上任意一點,且
的左、右焦點,P為橢圓C上任意一點,且 最小值為0.
最小值為0.查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省汕頭市金山中學高三(上)開學摸底數學試卷(文科)(解析版) 題型:解答題
 的左、右焦點,P為橢圓C上任意一點,且
的左、右焦點,P為橢圓C上任意一點,且 最小值為0.
最小值為0.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com