
【題目】現給出兩個條件:①![]() ,②
,②![]() ,從中選出一個條件補充在下面的問題中,并以此為依據求解問題:(選出一種可行的條件解答,若兩個都選,則按第一個解答計分)在
,從中選出一個條件補充在下面的問題中,并以此為依據求解問題:(選出一種可行的條件解答,若兩個都選,則按第一個解答計分)在![]() 中,
中,![]() 分別為內角
分別為內角![]() 所對的邊( ).
所對的邊( ).
(1)求![]() ;
;
(2)若![]() ,求
,求![]() 面積的最大值.
面積的最大值.
 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,已知圓![]() 的方程為
的方程為![]() ,圓
,圓![]() 的方程為
的方程為![]() ,動圓
,動圓![]() 與圓
與圓![]() 內切且與圓
內切且與圓![]() 外切.
外切.
(1)求動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)已知![]() 與
與![]() 為平面內的兩個定點,過
為平面內的兩個定點,過![]() 點的直線
點的直線![]() 與軌跡
與軌跡![]() 交于
交于![]() ,
,![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的離心率是
的離心率是![]() ,過點
,過點![]() 做斜率為
做斜率為![]() 的直線
的直線![]() ,橢圓
,橢圓![]() 與直線
與直線![]() 交于
交于![]() 兩點,當直線
兩點,當直線![]() 垂直于
垂直于![]() 軸時
軸時![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)當![]() 變化時,在
變化時,在![]() 軸上是否存在點
軸上是否存在點![]() ,使得
,使得![]() 是以
是以![]() 為底的等腰三角形,若存在求出
為底的等腰三角形,若存在求出![]() 的取值范圍,若不存在說明理由.
的取值范圍,若不存在說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果無窮數列{an}滿足條件:①![]() ;② 存在實數M,使得an≤M,其中n∈N*,那么我們稱數列{an}為Ω數列.
;② 存在實數M,使得an≤M,其中n∈N*,那么我們稱數列{an}為Ω數列.
(1)設數列{bn}的通項為bn=20n-2n,且是Ω數列,求M的取值范圍;
(2)設{cn}是各項為正數的等比數列,Sn是其前n項和,c3=![]() ,S3=
,S3=![]() ,證明:數列{Sn}是Ω數列;
,證明:數列{Sn}是Ω數列;
(3)設數列{dn}是各項均為正整數的Ω數列,求證:dn≤dn+1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,己知圓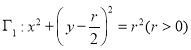 和雙曲線
和雙曲線![]() ,記
,記![]() 與
與![]() 軸正半軸、
軸正半軸、![]() 軸負半軸的公共點分別為
軸負半軸的公共點分別為![]() 、
、![]() ,又記
,又記![]() 與
與![]() 在第一、第四象限的公共點分別為
在第一、第四象限的公共點分別為![]() 、
、![]() .
.

(1)若![]() ,且
,且![]() 恰為
恰為![]() 的左焦點,求
的左焦點,求![]() 的兩條漸近線的方程;
的兩條漸近線的方程;
(2)若![]() ,且
,且![]() ,求實數
,求實數![]() 的值;
的值;
(3)若![]() 恰為
恰為![]() 的左焦點,求證:在
的左焦點,求證:在![]() 軸上不存在這樣的點
軸上不存在這樣的點![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠加工一批零件,加工過程中會產生次品,根據經驗可知,其次品率p與日產量x(萬件)之間滿足函數關系式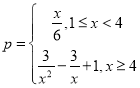 ,已知每生產1萬件合格品可獲利2萬元,但生產1萬件次品將虧損1萬元(次品率=次品數/生產量)
,已知每生產1萬件合格品可獲利2萬元,但生產1萬件次品將虧損1萬元(次品率=次品數/生產量)
(1)試寫出加工這批零件的日盈利額y(萬元)與日產量x(萬件)的函數;
(2)當日產量為多少時,可獲得最大利潤?最大利潤為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】自由購是一種通過自助結算購物的形式.某大型超市為調查顧客自由購的使用情況,隨機抽取了100人,調查結果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人數 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人數 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)現隨機抽取1名顧客,試估計該顧客年齡在[30,50)且未使用自由購的概率;
(2)從被抽取的年齡在[50,70]使用的自由購顧客中,隨機抽取2人進一步了解情況,求這2人年齡都在[50,60)的概率;
(3)為鼓勵顧客使用自由購,該超市擬對使用自由購顧客贈送1個環保購物袋.若某日該超市預計有5000人購物,試估計該超市當天至少應準備多少個環保購物袋?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過曲線C1:![]() (a>0,b>0)的左焦點F1作曲線C2:x2+y2=a2的切線,設切點為M,直線F1M交曲線C3:y2=2px(p>0)于點N,其中曲線C1與C3有一個共同的焦點,若|MF1|=|MN|,則曲線C1的離心率為( )
(a>0,b>0)的左焦點F1作曲線C2:x2+y2=a2的切線,設切點為M,直線F1M交曲線C3:y2=2px(p>0)于點N,其中曲線C1與C3有一個共同的焦點,若|MF1|=|MN|,則曲線C1的離心率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com