
(本題滿分16分)
如圖,橢圓C: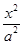 +
+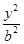 =1(a>b>0)的焦點F1,F2和短軸的一個端點A構成等邊三角形,
=1(a>b>0)的焦點F1,F2和短軸的一個端點A構成等邊三角形,
點(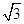 ,
,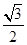 )在橢圓C上,直線l為橢圓C的左準線.
)在橢圓C上,直線l為橢圓C的左準線.
(1) 求橢圓C的方程;
(2) 點P是橢圓C上的動點,PQ ⊥l,垂足為Q.
是否存在點P,使得△F1PQ為等腰三角形?
若存在,求出點P的坐標;若不存在,說明理由.
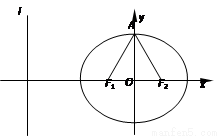
(1)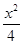 +
+ 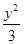 =1.(2)存在點P(-
=1.(2)存在點P(-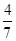 ,±
,±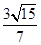 ),使△PF1Q為等腰三角形
),使△PF1Q為等腰三角形
【解析】本題主要考查了橢圓的標準方程.考查了學生綜合分析問題和解決問題的能力
(Ⅰ)設出橢圓方程,根據△AF1F2為正三角形可推斷出a和b的關系,設b2=3λ,a2=4λ,代入橢圓方程,進而把點(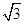 ,
,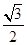 )代入即可求得λ,則橢圓的方程可得.
)代入即可求得λ,則橢圓的方程可得.
(Ⅱ)根據(1)可求得橢圓的離心率,進而求得PF1和PQ的關系,假設PF1=F1Q根據PF1= 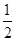 PQ推斷出PF1+F1Q=PQ,與“三角形兩邊之和大于第三邊”矛盾,假設不成立,再看若F1Q=PQ,設出P點坐標,則Q點坐標可得,進而表示出F1Q和PQ求得x和y的關系,與橢圓方程聯立求得P點坐標.判斷出存在點P,使得△PF1Q為等腰三角形。
PQ推斷出PF1+F1Q=PQ,與“三角形兩邊之和大于第三邊”矛盾,假設不成立,再看若F1Q=PQ,設出P點坐標,則Q點坐標可得,進而表示出F1Q和PQ求得x和y的關系,與橢圓方程聯立求得P點坐標.判斷出存在點P,使得△PF1Q為等腰三角形。
(1)橢圓C的方程為 +
+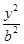 =1(a>b>0),由已知△AF1F2為正三角形,所以
=1(a>b>0),由已知△AF1F2為正三角形,所以
sin∠AF1O=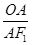 =
=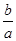 ,所以
,所以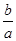 =
=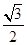 ,
,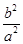 =
=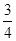 .
.
設b2=3λ,a2=4λ,橢圓方程為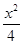 +
+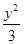 =λ.
=λ.
橢圓經過點(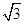 ,
,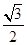 ),解得λ=1,所以橢圓C的方程為
),解得λ=1,所以橢圓C的方程為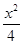 +
+ 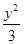 =1.
=1.
(2)由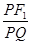 =e=
=e=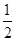 ,得PF1=
,得PF1=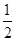 PQ.所以PF1≠PQ.
PQ.所以PF1≠PQ.
①若PF1=F1Q,則PF1+F1Q=PQ,與“三角形兩邊之和大于第三邊”矛盾,
所以PF1不可能與PQ相等
②若F1Q=PQ,設P(x,y)(x≠±2),則Q(-4,y).∴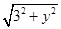 =4+x,
=4+x,
∴9+y2=16+8x+x2,又由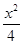 +
+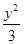 =1,得y2=3-
=1,得y2=3-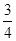 x2.
x2.
∴9+3-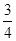 x2=16+8x+x2,∴
x2=16+8x+x2,∴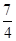 x2+8x+4=0.
x2+8x+4=0.
∴7x2+32x+16=0.∴x=-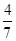 或x=-4.
或x=-4.
因為x∈(-2,2),所以x=-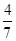 .所以P(-
.所以P(-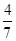 ,±
,±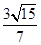 ).
).
存在點P(-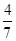 ,±
,±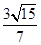 ),使△PF1Q為等腰三角形
),使△PF1Q為等腰三角形


科目:高中數學 來源: 題型:
| a1+2a2+3a3+…+nan |
| 1+2+3+…+n |
| n(n+1)(2n+1) |
| 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分16分)本題共有2個小題,第1小題滿分8分,第2小題滿分8分.
已知函數![]() (
(![]() ,
,![]() 、
、![]() 是常數,且
是常數,且![]() ),對定義域內任意
),對定義域內任意![]() (
(![]() 、
、![]() 且
且![]() ),恒有
),恒有![]() 成立.
成立.
(1)求函數![]() 的解析式,并寫出函數的定義域;
的解析式,并寫出函數的定義域;
(2)求![]() 的取值范圍,使得
的取值范圍,使得![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分16分)已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() .數列
.數列![]() 中,
中,![]() ,
,
![]()
![]() .(1)求數列
.(1)求數列![]() 的通項公式;(2)若存在常數
的通項公式;(2)若存在常數![]() 使數列
使數列![]() 是等比數列,求數列
是等比數列,求數列![]() 的通項公式;(3)求證:①
的通項公式;(3)求證:①![]() ;②
;②![]() .
.
查看答案和解析>>
科目:高中數學 來源:江蘇省私立無錫光華學校2009—2010學年高二第二學期期末考試 題型:解答題
本題滿分16分)已知圓內接四邊形ABCD的邊長分別為AB = 2,BC = 6,CD = DA = 4;求四邊形ABCD的面積.
查看答案和解析>>
科目:高中數學 來源:2010年上海市徐匯區高三第二次模擬考試數學卷(文) 題型:解答題
(本題滿分16分;第(1)小題5分,第(2)小題5分,第三小題6分)
已知函數 
(1)判斷并證明 在
在 上的單調性;
上的單調性;
(2)若存在 ,使
,使 ,則稱
,則稱 為函數
為函數 的不動點,現已知該函數有且僅有一個不動點,求
的不動點,現已知該函數有且僅有一個不動點,求 的值;
的值;
(3)若 在
在 上恒成立 , 求
上恒成立 , 求 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com