
【題目】如圖分別為定義域和值域均為![]() 的函數
的函數![]() 和函數
和函數![]() 的圖象,則下列命題正確的是( )
的圖象,則下列命題正確的是( )
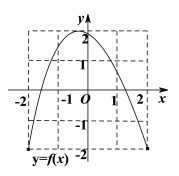
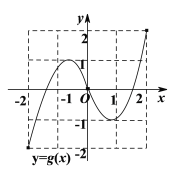
A.函數![]() 恰有
恰有![]() 個零點B.函數
個零點B.函數![]() 恰有
恰有![]() 個零點
個零點
C.函數![]() 恰有
恰有![]() 個零點D.函數
個零點D.函數![]() 恰有
恰有![]() 個零點
個零點
【答案】C
【解析】
將各選項中的復合函數分為內層函數和外層函數,先分析外層函數的零點及其范圍,再分析內層函數方程的根的個數,即可得出結論.
對于A選項,令![]() ,
,
則外層函數![]() 有
有![]() 個零點
個零點![]() ,
,![]() ,
,
關于![]() 的方程
的方程![]() 只有1個根,關于
只有1個根,關于![]() 的方程
的方程![]() 只有1個根,
只有1個根,
所以,函數![]() 恰有
恰有![]() 個零點,A選項錯誤;
個零點,A選項錯誤;
對于B選項,令![]() ,
,
則外層函數![]() 有
有![]() 個零點
個零點![]() ,
,![]() ,
,![]() ,
,
關于![]() 的方程
的方程![]() 有
有![]() 個根,關于
個根,關于![]() 的方程
的方程![]() 有
有![]() 個根,關于
個根,關于![]() 的方程
的方程![]() 有
有![]() 個根,
個根,
所以,函數![]() 恰有
恰有![]() 個零點,B選項錯誤;
個零點,B選項錯誤;
對于C選項,令![]() ,
,
則外層函數![]() 有
有![]() 個零點
個零點![]() ,
,![]() ,
,
關于![]() 的方程
的方程![]() 有
有![]() 個根,關于
個根,關于![]() 的方程
的方程![]() 有
有![]() 個根,
個根,
所以,函數![]() 恰有
恰有![]() 個零點,C選項正確;
個零點,C選項正確;
對于D選項,令![]() ,
,
則外層函數![]() 有
有![]() 個零點
個零點![]() ,
,![]() ,
,![]() ,
,
關![]() 的方程
的方程![]() 有
有![]() 個根,關
個根,關![]() 的方程
的方程![]() 有3個根,關于
有3個根,關于![]() 的方程
的方程![]() 有1個根,
有1個根,
所以,函數![]() 恰有
恰有![]() 個零點.
個零點.
故選:C.


科目:高中數學 來源: 題型:
【題目】橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,上、下頂點分別為
,上、下頂點分別為![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,
,![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過右焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,試探究在
兩點,試探究在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得可
,使得可![]() 為定值?若存在,求出點
為定值?若存在,求出點![]() 的坐標,若不存在,請說明理由?
的坐標,若不存在,請說明理由?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個摸球游戲,規則如下:在一不透明的紙盒中,裝有6個大小相同、顏色各異的玻璃球.參加者交費1元可玩1次游戲,從中有放回地摸球3次.參加者預先指定盒中的某一種顏色的玻璃球,然后摸球.當所指定的玻璃球不出現時,游戲費被沒收;當所指定的玻璃球出現1次,2次,3次時,參加者可相應獲得游戲費的0倍,1倍,![]() 倍的獎勵(
倍的獎勵(![]() ),且游戲費仍退還給參加者.記參加者玩1次游戲的收益為
),且游戲費仍退還給參加者.記參加者玩1次游戲的收益為![]() 元.
元.
(1)求概率![]() 的值;
的值;
(2)為使收益![]() 的數學期望不小于0元,求
的數學期望不小于0元,求![]() 的最小值.
的最小值.
(注:概率學源于賭博,請自覺遠離不正當的游戲!)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
(Ⅰ)若函數![]() 在其定義域上為單調函數,求
在其定義域上為單調函數,求![]() 的取值范圍;
的取值范圍;
(Ⅱ)若函數![]() 的圖像在
的圖像在![]() 處的切線的斜率為0,
處的切線的斜率為0,![]() ,已知
,已知![]() 求證:
求證:![]()
(Ⅲ)在(2)的條件下,試比較![]() 與
與![]() 的大小,并說明理由.
的大小,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校將甲、乙等6名新招聘的老師分配到4個不同的年級,每個年級至少分配1名教師,且甲、乙兩名老師必須分到同一個年級,則不同的分法種數為______
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知i為虛數單位,a為實數,復數z=(1﹣2i)(a+i)在復平面內對應的點為M,則![]() “”是“點M在第四象限”的( )
“”是“點M在第四象限”的( )
A.充分而不必要條件
B.必要而不充分條件
C.充要條件
D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,圓C的圓心坐標為(1,0),半徑為1.
(1)求圓C的極坐標方程;
(2)若以極點O為原點,極軸所在直線為x軸建立平面直角坐標系.已知直線l的參數方程為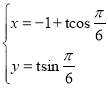 (t為參數),試判斷直線l與圓C的位置關系.
(t為參數),試判斷直線l與圓C的位置關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學生參加4門學科的學業水平測試,每門得![]() 等級的概率都是
等級的概率都是![]() ,該學生各學科等級成績彼此獨立.規定:有一門學科獲
,該學生各學科等級成績彼此獨立.規定:有一門學科獲![]() 等級加1分,有兩門學科獲
等級加1分,有兩門學科獲![]() 等級加2分,有三門學科獲
等級加2分,有三門學科獲![]() 等級加3分,四門學科全獲
等級加3分,四門學科全獲![]() 等級則加5分,記
等級則加5分,記![]() 表示該生的加分數,
表示該生的加分數, ![]() 表示該生獲
表示該生獲![]() 等級的學科門數與未獲
等級的學科門數與未獲![]() 等級學科門數的差的絕對值.
等級學科門數的差的絕對值.
(1)求![]() 的數學期望;
的數學期望;
(2)求![]() 的分布列.
的分布列.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com