
【題目】已知函數![]()
(Ⅰ)若函數![]() 在其定義域上為單調函數,求
在其定義域上為單調函數,求![]() 的取值范圍;
的取值范圍;
(Ⅱ)若函數![]() 的圖像在
的圖像在![]() 處的切線的斜率為0,
處的切線的斜率為0,![]() ,已知
,已知![]() 求證:
求證:![]()
(Ⅲ)在(2)的條件下,試比較![]() 與
與![]() 的大小,并說明理由.
的大小,并說明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)略;(Ⅲ)
;(Ⅱ)略;(Ⅲ)![]() <
<![]() .
.
【解析】
試題(Ⅰ)利用導數求解單調性,把恒成立轉化為最值;(Ⅱ)可用數學歸納法來證明![]() ;(Ⅲ)通過放縮法來解決
;(Ⅲ)通過放縮法來解決![]() 與
與![]() 的大小比較問題.
的大小比較問題.
試題解析:(Ⅰ) ∵f(1)="a-b=0" ∴a=b
∴![]()
∴![]()
要使函數![]() 在其定義域上為單調函數,則在定義域(0,+∞)內
在其定義域上為單調函數,則在定義域(0,+∞)內![]() 恒大于等于0或恒小于等于0,
恒大于等于0或恒小于等于0,
當a=0時,![]() 在(0,+∞)內恒成立;
在(0,+∞)內恒成立;
當a>0時,![]() 恒成立,則
恒成立,則![]() ∴
∴![]()
當a<0時,![]() 恒成立
恒成立
∴a的取值范圍是:![]()
(Ⅱ)![]() ∴a=1 則:
∴a=1 則:![]()
于是![]()
用數學歸納法證明![]() 如下:
如下:
當n=1時,![]() ,不等式成立;
,不等式成立;
假設當n=k時,不等式![]() 成立,即
成立,即![]() 也成立,
也成立,
當n=k+1時,![]()
所以當n=k+1時不等式成立,
綜上得對所有![]() 時,都有
時,都有![]()
(Ⅲ)由(2)得![]()
![]()
于是![]()
所以![]()
![]() ,
,![]()
累乘得:![]() 則
則![]()
所以![]()
![]()


科目:高中數學 來源: 題型:
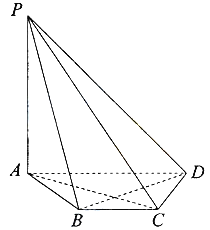
【題目】如圖,在四棱錐P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(Ⅰ)證明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直線PD與平面PAC所成的角為30°,求四棱錐P-ABCD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學大學畢業后,決定利用所學專業進行自主創業,經過市場調查,生產一小型電子產品需投入固定成本2萬元,每生產![]() 萬件,需另投入流動成本
萬件,需另投入流動成本![]() 萬元,當年產量小于
萬元,當年產量小于![]() 萬件時,
萬件時,![]() (萬元);當年產量不小于7萬件時,
(萬元);當年產量不小于7萬件時,![]() (萬元).已知每件產品售價為6元,假若該同學生產的商品當年能全部售完.
(萬元).已知每件產品售價為6元,假若該同學生產的商品當年能全部售完.
(1)寫出年利潤![]() (萬年)關于年產量
(萬年)關于年產量![]() (萬件)的函數解析式;(注:年利潤=年銷售收入-固定成本-流動成本)
(萬件)的函數解析式;(注:年利潤=年銷售收入-固定成本-流動成本)
(2)當年產量約為多少萬件時,該同學的這一產品所獲年利潤最大?最大年利潤是多少?
(取![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
甲、乙兩個籃球運動員互不影響地在同一位置投球,命中率分別為![]() 與
與![]() ,且乙投球2次均未命中的概率為
,且乙投球2次均未命中的概率為![]() .
.
(Ⅰ)求乙投球的命中率![]() ;
;
(Ⅱ)若甲投球1次,乙投球2次,兩人共命中的次數記為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從0,1,2,3,4這五個數中任選三個不同的數組成一個三位數,記X為所組成的三位數各位數字之和.
(1)求X是奇數的概率;
(2)求X的概率分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
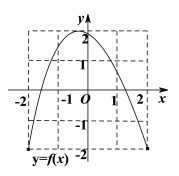
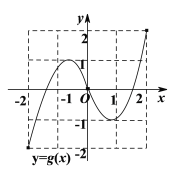
【題目】如圖分別為定義域和值域均為![]() 的函數
的函數![]() 和函數
和函數![]() 的圖象,則下列命題正確的是( )
的圖象,則下列命題正確的是( )
A.函數![]() 恰有
恰有![]() 個零點B.函數
個零點B.函數![]() 恰有
恰有![]() 個零點
個零點
C.函數![]() 恰有
恰有![]() 個零點D.函數
個零點D.函數![]() 恰有
恰有![]() 個零點
個零點
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分10分)選修4—4,坐標系與參數方程
已知曲線![]() ,直線
,直線![]() :
:![]() (
(![]() 為參數).
為參數).
(I)寫出曲線![]() 的參數方程,直線
的參數方程,直線![]() 的普通方程;
的普通方程;
(II)過曲線![]() 上任意一點
上任意一點![]() 作與
作與![]() 夾角為
夾角為![]() 的直線,交
的直線,交![]() 于點
于點![]() ,
,![]() 的最大值與最小值.
的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某公司舉行的年終慶典活動中,主持人利用隨機抽獎軟件進行抽獎:由電腦隨機生成一張如圖所示的3![]() 3表格,其中1格設獎300元,4格各設獎200元,其余4格各設獎100元,點擊某一格即顯示相應金額.某人在一張表中隨機不重復地點擊3格,記中獎的總金額為X元.
3表格,其中1格設獎300元,4格各設獎200元,其余4格各設獎100元,點擊某一格即顯示相應金額.某人在一張表中隨機不重復地點擊3格,記中獎的總金額為X元.
(1)求概率![]() ;
;
(2)求![]() 的概率分布及數學期望
的概率分布及數學期望![]() .
.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com