
【題目】若函數f(x)=(1﹣x2)(x2+ax+b)的圖象關于直線x=﹣2對稱,則f(x)的最大值為 .
【答案】16
【解析】解:∵函數f(x)=(1﹣x2)(x2+ax+b)的圖象關于直線x=﹣2對稱,
∴f(﹣1)=f(﹣3)=0且f(1)=f(﹣5)=0,
即[1﹣(﹣3)2][(﹣3)2+a(﹣3)+b]=0且[1﹣(﹣5)2][(﹣5)2+a(﹣5)+b]=0,
解之得 ![]() ,
,
因此,f(x)=(1﹣x2)(x2+8x+15)=﹣x4﹣8x3﹣14x2+8x+15,
求導數,得f′(x)=﹣4x3﹣24x2﹣28x+8,
令f′(x)=0,得x1=﹣2﹣ ![]() ,x2=﹣2,x3=﹣2+
,x2=﹣2,x3=﹣2+ ![]() ,
,
當x∈(﹣∞,﹣2﹣ ![]() )時,f′(x)>0;當x∈(﹣2﹣
)時,f′(x)>0;當x∈(﹣2﹣ ![]() ,﹣2)時,f′(x)<0;
,﹣2)時,f′(x)<0;
當x∈(﹣2,﹣2+ ![]() )時,f′(x)>0; 當x∈(﹣2+
)時,f′(x)>0; 當x∈(﹣2+ ![]() ,+∞)時,f′(x)<0
,+∞)時,f′(x)<0
∴f(x)在區間(﹣∞,﹣2﹣ ![]() )、(﹣2,﹣2+
)、(﹣2,﹣2+ ![]() )上是增函數,在區間(﹣2﹣
)上是增函數,在區間(﹣2﹣ ![]() ,﹣2)、(﹣2+
,﹣2)、(﹣2+ ![]() ,+∞)上是減函數.
,+∞)上是減函數.
又∵f(﹣2﹣ ![]() )=f(﹣2+
)=f(﹣2+ ![]() )=16,
)=16,
∴f(x)的最大值為16.
故答案為:16.
由題意得f(﹣1)=f(﹣3)=0且f(1)=f(﹣5)=0,由此求出a=8且b=15,由此可得f(x)=﹣x4﹣8x3﹣14x2+8x+15.利用導數研究f(x)的單調性,可得f(x)在區間(﹣∞,﹣2﹣ ![]() )、(﹣2,﹣2+
)、(﹣2,﹣2+ ![]() )上是增函數,在區間(﹣2﹣
)上是增函數,在區間(﹣2﹣ ![]() ,﹣2)、(﹣2+
,﹣2)、(﹣2+ ![]() ,+∞)上是減函數,結合f(﹣2﹣
,+∞)上是減函數,結合f(﹣2﹣ ![]() )=f(﹣2+
)=f(﹣2+ ![]() )=16,即可得到f(x)的最大值.
)=16,即可得到f(x)的最大值.


科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線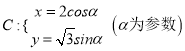 和定點
和定點![]() ,
, ![]() 是此曲線的左、右焦點,以原點
是此曲線的左、右焦點,以原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系.
軸正半軸為極軸,建立極坐標系.
(1)求直線![]() 的極坐標方程;
的極坐標方程;
(2)經過點![]() 且與直線
且與直線![]() 垂直的直線交此圓錐曲線于
垂直的直線交此圓錐曲線于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】f(x)是定義在(0,+∞)上的非負可導函數,且滿足xf′(x)+f(x)≤0,對任意正數a、b,若a<b,則必有( )
A.af(b)≤bf(a)
B.bf(a)≤af(b)
C.af(a)≤f(b)
D.bf(b)≤f(a)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知:如圖,兩同心圓: ![]() 和
和![]() .
. ![]() 為大圓上一動點,連結
為大圓上一動點,連結![]() (
(![]() 為坐標原點)交小圓于點
為坐標原點)交小圓于點![]() ,過點
,過點![]() 作
作![]() 軸垂線
軸垂線![]() (垂足為
(垂足為![]() ),再過點
),再過點![]() 作直線
作直線![]() 的垂線
的垂線![]() ,垂足為
,垂足為![]() .
.

(1)當點![]() 在大圓上運動時,求垂足
在大圓上運動時,求垂足![]() 的軌跡方程;
的軌跡方程;
(2)過點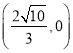 的直線
的直線![]() 交垂足
交垂足![]() 的軌跡于
的軌跡于![]() 兩點,若以
兩點,若以![]() 為直徑的圓與
為直徑的圓與![]() 軸相切,求直線
軸相切,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+bx﹣ ![]() (a>0),g(x)=4x+
(a>0),g(x)=4x+ ![]() +
+ ![]() ,且y=f(x+
,且y=f(x+ ![]() )為偶函數.設集合A={x|t﹣1≤x≤t+1}.
)為偶函數.設集合A={x|t﹣1≤x≤t+1}.
(1)若t=﹣ ![]() ,記f(x)在A上的最大值與最小值分別為M,N,求M﹣N;
,記f(x)在A上的最大值與最小值分別為M,N,求M﹣N;
(2)若對任意的實數t,總存在x1 , x2∈A,使得|f(x1)﹣f(x2)|≥g(x)對x∈[0,1]恒成立,試求a的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,a,b,c分別為內角A,B,C的對邊,且2asinA=(2b+c)sinB+(2c+b)sinC.
(1)求A的大小;
(2)求sinB+sinC的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是2017年第一季度五省![]() 情況圖,則下列陳述正確的是( )
情況圖,則下列陳述正確的是( )
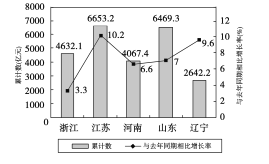
①2017年第一季度 ![]() 總量和增速均居同一位的省只有1個;
總量和增速均居同一位的省只有1個;
②與去年同期相比,2017年第一季度五個省的![]() 總量均實現了增長;
總量均實現了增長;
③去年同期的![]() 總量前三位是江蘇、山東、浙江;
總量前三位是江蘇、山東、浙江;
④2016年同期浙江的![]() 總量也是第三位.
總量也是第三位.
A. ①② B. ②③④ C. ②④ D. ①③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com