
【題目】如圖是函數![]() 的導函數
的導函數![]() 的圖象,給出下列命題:
的圖象,給出下列命題:

①-2是函數![]() 的極值點;
的極值點;
②![]() 是函數
是函數![]() 的極值點;
的極值點;
③![]() 在
在![]() 處取得極大值;
處取得極大值;
④函數![]() 在區間
在區間![]() 上單調遞增.則正確命題的序號是
上單調遞增.則正確命題的序號是
A. ①③ B. ②④ C. ②③ D. ①④
【答案】D
【解析】分析:由條件利用導函數的圖象特征,利用導數研究函數的單調性和極值,逐一判斷各個選項是否正確,從而得出結論.
詳解:
根據導函數y=f′(x)的圖象可得,y=f′(x)在(﹣∞,﹣2)上大于零,在(﹣2,2)、(2,+∞)上大于零,
且f′(﹣2)=0,
故函數f(x)在(﹣∞,﹣2)上為減函數,在(﹣2,+∞)、(2,+∞)上為增函數.
故﹣2是函數y=f(x)的極小值點,故①正確;
故1不是函數y=f(x)的極值點,故②不正確;
根據函數-1的兩側均為單調遞增函數,故-1不是極值點.
根據y=f(x)=在區間(﹣2,2)上的導數大于或等于零,故f(x)在區間(﹣2,2)上單調遞增,故④正確,
故選:D.


科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0),e=
=1(a>b>0),e= ![]() ,其中F是橢圓的右焦點,焦距為2,直線l與橢圓C交于點A、B,點A,B的中點橫坐標為
,其中F是橢圓的右焦點,焦距為2,直線l與橢圓C交于點A、B,點A,B的中點橫坐標為 ![]() ,且
,且 ![]() =λ
=λ ![]() (其中λ>1).
(其中λ>1).
(1)求橢圓C的標準方程;
(2)求實數λ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年6月14日,世界杯足球賽在俄羅斯拉開帷幕.通過隨機調查某小區100名性別不同的居民是否觀看世界杯比賽,得到以下列聯表:
觀看世界杯 | 不觀看世界杯 | 總計 | |
男 | 40 | 20 | 60 |
女 | 15 | 25 | 40 |
總計 | 55 | 45 | 100 |
經計算![]() 的觀測值
的觀測值![]() .
.
附表:
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參照附表,所得結論正確的是( )
A. 有![]() 以上的把握認為“該小區居民是否觀看世界杯與性別有關”
以上的把握認為“該小區居民是否觀看世界杯與性別有關”
B. 有![]() 以上的把握認為“該小區居民是否觀看世界杯與性別無關”
以上的把握認為“該小區居民是否觀看世界杯與性別無關”
C. 在犯錯誤的概率不超過0.005的前提下,認為“該小區居民是否觀看世界杯與性別有關”
D. 在犯錯誤的概率不超過0.001的前提下,認為“該小區居民是否觀看世界杯與性別無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《厲害了,我的國》這部電影記錄:到2017年底,我國高鐵營運里程達2.5萬公里,位居世界第一位,超過第二名至第十名的總和,約占世界高鐵總量的三分之二.如圖是我國2009年至2017年高鐵營運里程(單位:萬公里)的折線圖.

根據這9年的高鐵營運里程,甲、乙兩位同學分別選擇了![]() 與時間變量
與時間變量![]() 的兩個回歸模型①:
的兩個回歸模型①:![]() ;②
;②![]() .
.
(1)求![]() ,
,![]() (精確到0.01);
(精確到0.01);
(2)乙求得模型②的回歸方程為![]() ,你認為哪個模型的擬合效果更好?并說明理由.
,你認為哪個模型的擬合效果更好?并說明理由.
附:參考公式: ,
,![]() ,
,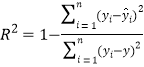 .
.
參考數據:
|
|
|
|
|
|
1.39 | 76.94 | 285 | 0.22 | 0.09 | 3.72 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a>0,函數 ![]() .
.
(1)記f(x)在區間[0,4]上的最大值為g(a),求g(a)的表達式;
(2)是否存在a使函數y=f(x)在區間(0,4)內的圖象上存在兩點,在該兩點處的切線互相垂直?若存在,求出a的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C對應的邊分別是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面積S=5 ![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某個產品有若千零部件構成,加工時需要經過6道工序,分別記為![]() .其中,有些工序因為是制造不同的零部件,所以可以在幾臺機器上同時加工;有些工序因為是對同一個零部件進行處理,所以存在加工順序關系.若加工工序
.其中,有些工序因為是制造不同的零部件,所以可以在幾臺機器上同時加工;有些工序因為是對同一個零部件進行處理,所以存在加工順序關系.若加工工序![]() 必須要在工序
必須要在工序![]() 完成后才能開工,則稱
完成后才能開工,則稱![]() 為
為![]() 的緊前工序.現將各工序的加工次序及所需時間(單位:小時)列表如下:
的緊前工序.現將各工序的加工次序及所需時間(單位:小時)列表如下:
工序 |
|
|
|
|
|
|
加工時間 | 3 | 4 | 2 | 2 | 2 | 1 |
緊前工序 | 無 |
| 無 |
|
|
|
現有兩臺性能相同的生產機器同時加工該產品,則完成該產品的最短加工時間是__________小時.(假定每道工序只能安排在一臺機器上,且不能間斷).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com