
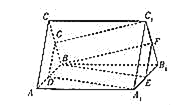
【題目】如圖所示,三棱柱ABC﹣A1B1C1的側棱垂直于底面,且底面是邊長為2的正三角形,AA1=3,點D,E,F,G分別是所在棱的中點.
(Ⅰ)證明:平面BEF∥平面DA1C1;
(Ⅱ)求三棱柱ABC﹣A1B1C1夾在平面BEF和平面DA1C1之間的部分的體積.
附:臺體的體積![]() ,其中S和S′分別是上、下底面面積,h是臺體的高.
,其中S和S′分別是上、下底面面積,h是臺體的高.
【答案】(Ⅰ)見解析(Ⅱ)![]()
【解析】
(Ⅰ)分別證明EF∥平面DA1C1和BE∥平面DA1C1,即可得證;
(Ⅱ)可看作三棱臺DBG﹣A1B1C1減掉三棱錐B﹣B1EF剩余部分,分別計算,求差即可.
證明:(Ⅰ)∵E,F分別是A1 B1和B1C1的中點,∴EF∥A1C1,
∵EF平面DA1C1,A1C1平面DA1C1,
∴EF∥平面DA1C1,
∵D,E分別是AB和A1B1的中點,∴![]() ,
,
∴四邊形BDA1E是平行四邊形,∴BE∥A1D,
∵BE 平面DA1C1,A1D 平面DA1C1,
∴BE∥平面DA1C1,
∵BE∩EF=E,∴平面BEF∥平面DA1C1.
(Ⅱ)由圖可知,三棱柱ABC﹣A1B1C1夾在平面BEF和平面DA1C1之間的部分,
可看作三棱臺DBG﹣A1B1C1減掉三棱錐B﹣B1EF剩余部分,
∵三棱柱ABC﹣A1B1C1夾在平面BEF和平面DA1C1之間的部分的體積.
![]() ,
,
∴三棱臺DBG﹣A1B1C1的體積為:![]() ,
,
三棱錐B﹣B1EF體積![]() ,
,
∴三棱柱ABC﹣A1B1C1夾在平面BEF和平面DA1C1之間的部分的體積:![]() .
.


 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:高中數學 來源: 題型:
【題目】某學校為調查高二年級學生的身高情況,按隨機抽樣的方法抽取80名學生,得到男生身高情況的頻率分布直方圖(圖(1))和女生身高情況的頻率分布直方圖(圖(2)).已知圖(1)中身高(單位:![]() )在
)在![]() 內的男生人數有16人.
內的男生人數有16人.
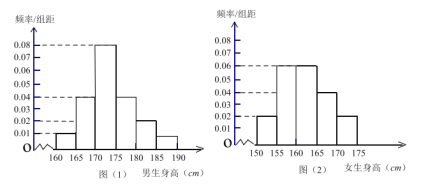
(Ⅰ)求在抽取的學生中,男女生各有多少人?
(Ⅱ)根據頻率分布直方圖,完成下列的![]() 列聯表,并判斷能有多大(百分之幾)的把握認為“身高與性別有關”?
列聯表,并判斷能有多大(百分之幾)的把握認為“身高與性別有關”?
|
| 總計 | |
男生人數 | |||
女生人數 | |||
總計 |
附:參考公式和臨界值表:
 ,
,
| 5.024 | 6.635 | 7.879 | 10.828 |
| 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E:![]() 的左、右焦點分別為F1,F2,離心率為
的左、右焦點分別為F1,F2,離心率為![]() ,點A在橢圓E上,∠F1AF2=60°,△F1AF2的面積為4
,點A在橢圓E上,∠F1AF2=60°,△F1AF2的面積為4![]() .
.
(1)求橢圓E的方程;
(2)過原點O的兩條互相垂直的射線與橢圓E分別交于P,Q兩點,證明:點O到直線PQ的距離為定值,并求出這個定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某社區為了解居民參加體育鍛煉情況,隨機抽取18名男性居民,12名女性居民對他們參加體育鍛煉的情況進行問卷調查.現按參加體育鍛煉的情況將居民分成3類:甲類(不參加體育鍛煉),乙類(參加體育鍛煉,但平均每周參加體育鍛煉的時間不超過5個小時),丙類(參加體育鍛煉,且平均每周參加體育鍛煉的時間超過5個小時),調查結果如下表:
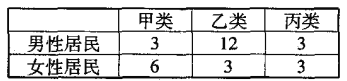
(1)根據表中的統計數據,完成下面列聯表,并判斷是否有![]() 的把握認為參加體育鍛煉與否與性別有關?
的把握認為參加體育鍛煉與否與性別有關?
(2)從抽出的女性居民中再隨機抽取2人進一步了解情況,求所抽取的2人中乙類,丙類各有1人的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的離心率為
的離心率為![]() ,圓
,圓![]() 與
與![]() 軸正半軸交于點
軸正半軸交于點![]() , 圓
, 圓![]() 在點
在點![]() 處的切線被橢圓
處的切線被橢圓![]() 截得的弦長為
截得的弦長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設圓![]() 上任意一點
上任意一點![]() 處的切線交橢圓
處的切線交橢圓![]() 于點
于點![]() 、
、![]() ,求證:
,求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+ax﹣1(a∈R).
(Ⅰ)當a=1時,求f(x)>0的解集;
(Ⅱ)對于任意x∈R,不等式f(x)<0恒成立,求a的取值范圍;
(Ⅲ)求關于x的不等式f(x)<0的解集.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的首項為1,若對任意的n∈N*,數列{an}滿足an+1﹣3an<2,則稱數列{an}具有性質L.
(Ⅰ)判斷下面兩個數列是否具有性質L:
①1,3,5,7,9,…;
②1,4,16,64,256,…;
(Ⅱ)若{an}是等差數列且具有性質L,其前n項和Sn滿足Sn<2n2+2n(n∈N*),求數列{an}的公差d的取值范圍;
(Ⅲ)若{an}是公比為正整數的等比數列且具有性質L,設bn=an![]() (n∈N*),且數列{bn}不具有性質L,求數列{an}的通項公式.
(n∈N*),且數列{bn}不具有性質L,求數列{an}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,其中
,其中![]() 為自然對數的底數.
為自然對數的底數.
(Ⅰ)當![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(Ⅱ)求函數![]() 的單調區間;
的單調區間;
(Ⅲ)用![]() 表示
表示![]() ,
,![]() 中的較大者,記函數
中的較大者,記函數![]() .若函數
.若函數![]() 在
在![]() 內恰有2個零點,求實數
內恰有2個零點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P-ABC中,PA⊥底面ABC,AC⊥BC,H為PC的中點,M為AH中點,PA=AC=2,BC=1.
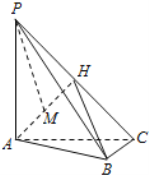
(Ⅰ)求證:AH⊥平面PBC;
(Ⅱ)求PM與平面AHB成角的正弦值;
(Ⅲ)在線段PB上是否存在點N,使得MN∥平面ABC,若存在,請說明點N的位置,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com