
【題目】在四棱柱 ![]() 中,底面
中,底面 ![]() 為矩形,面
為矩形,面 ![]() ⊥平面
⊥平面 ![]() ,
, ![]() =
= ![]() =
= ![]() =
= ![]() ,
, ![]() =2,
=2, ![]() 是
是 ![]() 的中點.
的中點.
(Ⅰ)求證: ![]() ⊥
⊥ ![]() ;
;
(Ⅱ)求BD與平面 ![]() 所成角的正弦值.
所成角的正弦值.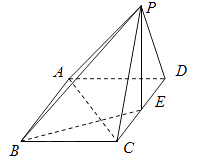
【答案】(Ⅰ)∵PD=PC,E為CD的中點,∴PE⊥CD,
∵平面PCD⊥平面ABCD,
∴PE⊥平面ABCD,
∴PE⊥AC,
在Rt ![]() 中,
中, ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴BE⊥CA,
∵BE ![]() PE=E,
PE=E,
∴AC⊥平面PBE,
∴AC⊥PB;
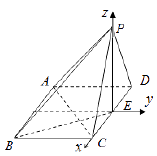
(Ⅱ)以E為坐標原點,如圖建立空間直角坐標系,則 P(0,0,1),C(1,0,0), D(-1,0,0)
, ![]() 則
則 ![]() ,
, ![]() ,
,
設平面PAB的法向量為 ![]() ,則
,則 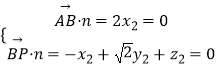 ,取
,取 ![]() ,則
,則 ![]() ,
, ![]() ,∴
,∴ ![]() .
.
設 BD 與平面PAB 所成角為 ![]() ,
,
則 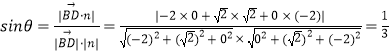
∴BD 與平面PAB 所成角的正弦值為 ![]() .
.
【解析】(1)證AC垂直面PBC即可得到AC垂直PB;
(2)建立空間坐標系,找到BD的方向向量、平面PAB的法向量,然后算出夾角.


 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x+1|,g(x)=2|x|+a.
(Ⅰ)當a=0時,解不等式f(x)≥g(x);
(Ⅱ)若存在x∈R,使得f(x)≥g(x)成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果執行如圖所示的程序框圖,輸入正整數N(N≥2)和實數a1 , a2 , …,an , 輸出A,B,則( ) 
A.A和B分別是a1 , a2 , …,an中最小的數和最大的數
B.A和B分別是a1 , a2 , …,an中最大的數和最小的數
C.![]() 為a1 , a2 , …,an的算術平均數
為a1 , a2 , …,an的算術平均數
D.A+B為a1 , a2 , …,an的和
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)的右焦點為(
=1(a>b>0)的右焦點為( ![]() ,0),離心率為
,0),離心率為 ![]() .
.
(1)求橢圓C的標準方程;
(2)若動點P(x0 , y0)為橢圓C外一點,且點P到橢圓C的兩條切線相互垂直,求點P的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】動點 ![]() 與定點
與定點 ![]() 的距離和它到定直線
的距離和它到定直線 ![]() 的距離的比是
的距離的比是 ![]() ∶
∶ ![]() ,記點
,記點 ![]() 的軌跡為
的軌跡為 ![]() .
.
(1)求曲線 ![]() 的方程;
的方程;
(2)對于定點 ![]() ,作過點
,作過點 ![]() 的直線
的直線 ![]() 與曲線
與曲線 ![]() 交于不同的兩點
交于不同的兩點 ![]() ,
, ![]() ,求△
,求△ ![]() 的內切圓半徑的最大值.
的內切圓半徑的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有10個不同的產品,其中4個次品,6個正品.現每次取其中一個進行測試,直到4個次品全測完為止,若最后一個次品恰好在第五次測試時被發現,則該情況出現的概率是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1中,側面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC, 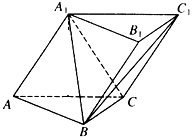
(Ⅰ)求證:AC⊥A1B;
(Ⅱ)求二面角A﹣A1C﹣B的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2ax(a>0).
(1)當a=2時,解關于x的不等式﹣3<f(x)<5;
(2)對于給定的正數a,有一個最大的正數M(a),使得在整個區間[0,M(a)]上,不等式|f(x)|≤5恒成立.求出M(a)的解析式;
(3)函數y=f(x)在[t,t+2]的最大值為0,最小值是﹣4,求實數a和t的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com