Question

【題目】如圖所示，在四棱錐 中，底面 為正方形， 平面 ，且 ，點 在線段 上，且 .

（Ⅰ）證明：平面 平面 ；
（Ⅱ）求四棱錐 的體積.

Answer 1

【答案】解：（Ⅰ）證明：∵ 平面 ， 平面 ，
∴ .
又∵底面 為正方形，
∴ .
∵ ，
∴ 平面 .
∴ .
設(shè) 交 于點 ，如圖，在 中，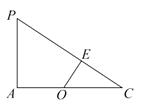

∵ ， ， ，
∴由余弦定理可得 .
∴ .
∴ .
∵ ， 平面 ， 平面 ，
∴ 平面 .
又∵ 在平面 內(nèi)，
∴平面 平面 ；
（Ⅱ）由題意可得 ，
而 ， 為三棱錐 的高，
則
【解析】（Ⅰ）先由線面垂直的性質(zhì)證出P A ⊥ B D與B D ⊥ A C，再由線面垂直的判定定理證明線面垂直即可得到平面 B D E ⊥ 平面 P C D ；
（Ⅱ）設(shè)AC與BD的交點為O，連結(jié)OE，利用VE-ABCD=SP-ABCD ， 可求四棱錐的體積．