
| A. | $(\frac{2}{e},\frac{3}{4})$ | B. | $[\frac{2}{e},\frac{3}{4})$ | C. | $(\frac{2}{e},1)$ | D. | $[\frac{2}{e},1)$ |
分析 設g(x)=ex(3x-1),h(x)=ax-a,對g(x)求導,將問題轉化為存在唯一的整數x0使得g(x0)在直線h(x)=ax-a的下方,求導數可得函數的極值,解g(-1)-h(-1)=-4e-1+2a≥0,求得a的取值范圍.
解答 解:設g(x)=ex(3x-1),h(x)=ax-a,
則g′(x)=ex(3x+2),
∴x∈(-∞,-$\frac{2}{3}$),g′(x)<0,g(x)單調遞減,
x∈(-$\frac{2}{3}$,+∞),g′(x)>0,g(x)單調遞增,
∴x=-$\frac{2}{3}$,取最小值-3e-$\frac{2}{3}$,
∴g(0)=-1<-a=h(0),
g(1)-h(1)=2e>0,
直線h(x)=ax-a恒過定點(1,0)且斜率為a,
∴g(-1)-h(-1)=-4e-1+2a>0,
∴a>$\frac{2}{e}$,
a<1,
∴a的取值范圍($\frac{2}{e}$,1).
故選:C.
點評 本題考查求函數的導數,利用導數判斷函數的單調性和極值問題,涉及轉化的思想,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
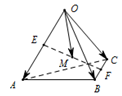 如圖,E,F分別是四面體OABC的邊OA,BC的中點,M為EF的中點,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,則下列向量中與$\overrightarrow{OM}$相等的向量是( )
如圖,E,F分別是四面體OABC的邊OA,BC的中點,M為EF的中點,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,則下列向量中與$\overrightarrow{OM}$相等的向量是( )| A. | -$\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | B. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | C. | $\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | D. | -$\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
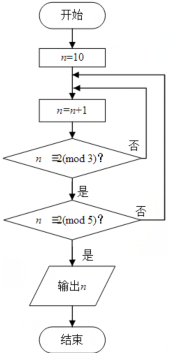 若正整數N除以正整數m后的余數為n,則記為N=n( mod m),例如10=2(mod 4).如圖程序框圖的算法源于我國古代聞名中外的《中國剩余定理》.執行該程序框圖,則輸出的n等于( )
若正整數N除以正整數m后的余數為n,則記為N=n( mod m),例如10=2(mod 4).如圖程序框圖的算法源于我國古代聞名中外的《中國剩余定理》.執行該程序框圖,則輸出的n等于( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com