Question

試求過P（3，5）且與曲線y=x²相切的切線方程.

Answer 1

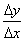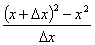解：y′===2x.

設所求切線的切點為A（x₀，y₀）.

∵點A在曲線y=x²上，

∴y₀=x₀².

又∵A是切點，

∴過點A的切線的斜率y′|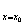=2x₀.

∵所求的切線過P（3，5）和A（x₀，y₀）兩點，

∴其斜率又為，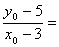

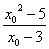∴2x₀=，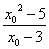

解之得x₀=1或x₀=5.

從而切點A的坐標為（1，1）或（5，25）.

當切點為（1，1）時，切線的斜率為k₁=2x₀=2；

當切點為（5，25）時，切線的斜率為k₂=2x₀=10.

∴所求的切線有兩條，方程分別為y-1=2（x-1）和y-25=10（x-5），

即y=2x-1和y=10x-25.