
分析 (1)求出函數的導數,利用函數的極值點,求解b,然后驗證求解函數的單調區間.
(2)求出函數的導數,利用函數的單調性求解函數的最值,推出結果即可.
解答 解:(1)因為x=1是$f(x)=2x+\frac{b}{x}+lnx$的一個極值點,
所以f′(1)=0,解得b=3,經檢驗,適合題意,所以b=3-------------------------(2分)
定義域為(0,+∞),f′(x)=2-$\frac{3}{{x}^{2}}$+$\frac{1}{x}$<0,解得x∈(-$\frac{3}{2}$,1)------------(4分)
所以函數的單調遞減區間為:(0,1]-------------------------------------(6分)
(2)$g(x)=f(x)-\frac{3+a}{x}=2x+lnx-\frac{a}{x}$,$g'(x)=2+\frac{1}{x}+\frac{a}{x^2}$--------(8分)
因為函數在[1,2]上單調遞增,所以g'(x)≥0恒成立,即$2+\frac{1}{x}+\frac{a}{x^2}≥0$恒成立
所以a≥-2x2-x,即a≥(-2x2-x)max--------(10分)
而在[1,2]上(-2x2-x)max=-3
所以a≥-3--------(12分).
點評 本題考查函數的導數的綜合應用,函數的極值以及函數的單調性函數的最值的求法,考查轉化思想以及計算能力.


 精英口算卡系列答案
精英口算卡系列答案科目:高中數學 來源: 題型:解答題
 在平面直角坐標系xOy中,已知橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,其焦點與橢圓上最近點的距離為2-$\sqrt{2}$.
在平面直角坐標系xOy中,已知橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,其焦點與橢圓上最近點的距離為2-$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
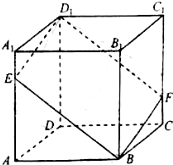 已知正方體ABCD-A1B1C1D1,如圖,E是棱AA1上動點,過點D1,E,B作該正方體的截面與棱CC1交于點F.設AE=x,則下列關于四棱錐B1-BFD1E的命題,其中正確的序號有③④
已知正方體ABCD-A1B1C1D1,如圖,E是棱AA1上動點,過點D1,E,B作該正方體的截面與棱CC1交于點F.設AE=x,則下列關于四棱錐B1-BFD1E的命題,其中正確的序號有③④查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com