
【題目】已知橢圓 ![]() 的半焦距為
的半焦距為 ![]() ,原點
,原點 ![]() 到經過兩點
到經過兩點 ![]() 的直線的距離為
的直線的距離為 ![]() .
.
(Ⅰ)求橢圓 ![]() 的離心率;
的離心率;
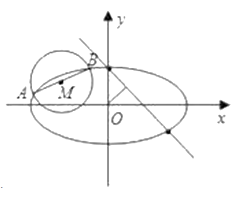
(Ⅱ)如圖, ![]() 是圓
是圓 ![]() 的一條直徑,若橢圓
的一條直徑,若橢圓 ![]() 經過
經過 ![]() 兩點,求橢圓
兩點,求橢圓 ![]() 的方程.
的方程.
【答案】解:(Ⅰ)過點 ![]() 的直線方程為
的直線方程為 ![]() ,
,
則原點 ![]() 到直線的距離
到直線的距離 ![]() ,
,
由 ![]() ,得
,得 ![]() ,解得離心率
,解得離心率 ![]() .
.
(Ⅱ)由(1)知,橢圓 ![]() 的方程為
的方程為 ![]() .
.
依題意,圓心 ![]() 是線段
是線段 ![]() 的中點,且
的中點,且 ![]() .
.
易知, ![]() 不與
不與 ![]() 軸垂直.
軸垂直.
設其直線方程為 ![]() ,代入(1)得
,代入(1)得
![]() .
.
設 ![]() ,則
,則 ![]() ,
, ![]() .
.
由 ![]() ,得
,得 ![]() ,解得
,解得 ![]() .
.
從而 ![]() .
.
于是 ![]() .
.
由 ![]() ,得
,得 ![]() ,解得
,解得 ![]() .
.
故橢圓 ![]() 的方程為
的方程為 ![]() .
.
【解析】(1)根據題意由點到直線的距離公式![]() 可得出
可得出![]() 代入
代入![]() ,聯立可求出離心率即可。(2)由(1)設出橢圓的方程再設出直線AB的方程聯立,借助韋達定理求出x1 + x2、x1x2關于k的代數式代入到弦長公式中即可求出b2的值,進而得到橢圓的方程。
,聯立可求出離心率即可。(2)由(1)設出橢圓的方程再設出直線AB的方程聯立,借助韋達定理求出x1 + x2、x1x2關于k的代數式代入到弦長公式中即可求出b2的值,進而得到橢圓的方程。
【考點精析】通過靈活運用點到直線的距離公式和橢圓的標準方程,掌握點![]() 到直線
到直線![]() 的距離為:
的距離為: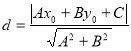 ;橢圓標準方程焦點在x軸:
;橢圓標準方程焦點在x軸:![]() ,焦點在y軸:
,焦點在y軸:![]() 即可以解答此題.
即可以解答此題.


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD為梯形,CD∥AB,AB=2CD,AC交BD于O,銳角△PAD所在平面⊥底面ABCD,PA⊥BD,點Q在側棱PC上,且PQ=2QC.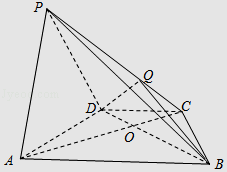
(1)求證:PA∥平面QBD;
(2)求證BD⊥AD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的一系列對應值如下表:
的一系列對應值如下表:

(1)根據表格提供的數據求出函數![]() 的一個解析式;
的一個解析式;
(2)根據(1)的結果,若函數![]() 的周期為
的周期為![]() ,當
,當![]() 時,方程
時,方程![]() 恰有兩個不同的解,求實數
恰有兩個不同的解,求實數![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從2017年1月18日開始,支付寶用戶可以通過“![]() 掃‘福’字”和“參與螞蟻森林”兩種方式獲得福卡(愛國福、富強福、和諧福、友善福,敬業福),除夕夜
掃‘福’字”和“參與螞蟻森林”兩種方式獲得福卡(愛國福、富強福、和諧福、友善福,敬業福),除夕夜![]() ,每一位提前集齊五福的用戶都將獲得一份現金紅包.某髙校一個社團在年后開學后隨機調査了80位該校在讀大學生,就除夕夜
,每一位提前集齊五福的用戶都將獲得一份現金紅包.某髙校一個社團在年后開學后隨機調査了80位該校在讀大學生,就除夕夜![]() 之前是否集齊五福進行了一次調查(若未參與集五福的活動,則也等同于未集齊五福),得到具體數據如下表:
之前是否集齊五福進行了一次調查(若未參與集五福的活動,則也等同于未集齊五福),得到具體數據如下表:
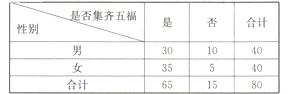
(1)計算這80位大學生集齊五福的頻率,并據此估算該校10000名在讀大學生中集齊五福的人數;
(2)為了解集齊五福的大學生明年是否愿意繼續參加集五福活動,該大學的學生會從集齊五福的學生中,選取2位男生和3位女生逐個進行采訪,最后再隨機選取3次采訪記錄放到該大學的官方網站上,求最后被選取的3次采訪對象中至少有一位男生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2eax .
(Ⅰ)當a<0時,討論函數f(x)的單調性;
(Ⅱ)在(1)條件下,求函數f(x)在區間[0,1]上的最大值;
(Ⅲ)設函數g(x)=2ex﹣ ![]() ,求證:當a=1,對x∈(0,1),g(x)﹣xf(x)>2恒成立.
,求證:當a=1,對x∈(0,1),g(x)﹣xf(x)>2恒成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】命題p:x∈(﹣∞,0),2x>3x;命題q:x∈(0,+∞), ![]() >x3; 則下列命題中真命題是( )
>x3; 則下列命題中真命題是( )
A.p∧q
B.(¬p)∧q
C.(¬p)∨(¬q)
D.p∧(¬q)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=Asin(x+φ)(A>0,0<<4,|φ|< ![]() )過點(0,
)過點(0, ![]() ),且當x=
),且當x= ![]() 時,函數f(x)取得最大值1.
時,函數f(x)取得最大值1.
(1)將函數f(x)的圖象向右平移 ![]() 個單位得到函數g(x),求函數g(x)的表達式;
個單位得到函數g(x),求函數g(x)的表達式;
(2)在(1)的條件下,函數h(x)=f(x)+g(x)+2cos2x﹣1,如果對于x1 , x2∈R,都有h(x1)≤h(x)≤h(x2),求|x1﹣x2|的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若分別為P(1,0)、Q(2,0),R(4,0)、S(8,0)四個點各作一條直線,所得四條直線恰圍成正方形,則該正方形的面積不可能為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com