
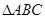 分割成16個全等的小正三角形,在每個三角形的頂點各放置一個數,使位于同一直線上的點放置的數(當數的個數不少于3時)都分別依次成等差數列,若頂點
分割成16個全等的小正三角形,在每個三角形的頂點各放置一個數,使位于同一直線上的點放置的數(當數的個數不少于3時)都分別依次成等差數列,若頂點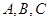 處的三個數互不相同且和為1,則所有頂點的數之和
處的三個數互不相同且和為1,則所有頂點的數之和 .
.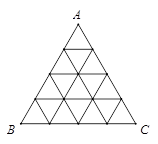
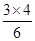 ,當n=3時,根據等差數列的性質可得,A+B=D+E,A+C=I+H,B+C=F+G,且A+B+C=1,從而可得D+E+H+I+F+F=2(A+B+C)=2,同樣根據等差中項可得,M的數為
,當n=3時,根據等差數列的性質可得,A+B=D+E,A+C=I+H,B+C=F+G,且A+B+C=1,從而可得D+E+H+I+F+F=2(A+B+C)=2,同樣根據等差中項可得,M的數為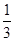 ,所以
,所以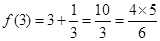 ,依次可知結論為
,依次可知結論為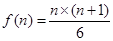 ,那么可知頂點
,那么可知頂點 處的三個數互不相同且和為1,則n=5時,所有頂點的數之和
處的三個數互不相同且和為1,則n=5時,所有頂點的數之和 5,故答案為5.
5,故答案為5.

 補充習題江蘇系列答案
補充習題江蘇系列答案 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:高中數學 來源:不詳 題型:解答題
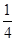 an bn,求數列{cn}的前n項和Tn.
an bn,求數列{cn}的前n項和Tn.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com