解:(1)∵

=(cosωx,2cosωx),

=(2cosωx,sinωx)
∴函數(shù)f(x)=

+1=2cos
2ωx+2sinωx•cosωx+1
=cos2ωx+1+sin2ωx+1
=

sin(2ωx+

)+2
∵函數(shù)f(x)的最小正周期是

即

=

∴ω=2
(2)由(1)可得f(x)=

sin(4x+

)+2
故當4x+

=

+2kπ,k∈Z時,函數(shù)取最大值2+

此時x∈{x|x=
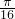
+

π,k∈Z}
分析:(1)由已知中

=(cosωx,2cosωx),

=(2cosωx,sinωx),結合函數(shù)f(x)=

+1和平面向量數(shù)量積公式,我們易求出函數(shù)的解析式,進而根據(jù)函數(shù)f(x)的最小正周期是

,進而求出ω的值;
(2)根據(jù)(1)中的函數(shù)的解析式,結合正弦型函數(shù)的性質(zhì),我們易得到(x)的最大值,及f(x)取得最大值的x的集合.
點評:本題考查的知識點是平面向量的數(shù)量積公式,正弦型函數(shù)的單調(diào)性與ω的關系,正弦型的最值,其中根據(jù)平面向量的數(shù)量積公式,求出函數(shù)的解析式,是解答本題的關鍵.

 =(cosωx,2cosωx),
=(cosωx,2cosωx), =(2cosωx,sinωx)(x∈R,ω>0),已知函數(shù)f(x)=
=(2cosωx,sinωx)(x∈R,ω>0),已知函數(shù)f(x)= +1的最小正周期是
+1的最小正周期是 .
. =(cosωx,2cosωx),
=(cosωx,2cosωx), =(2cosωx,sinωx)
=(2cosωx,sinωx) +1=2cos2ωx+2sinωx•cosωx+1
+1=2cos2ωx+2sinωx•cosωx+1 sin(2ωx+
sin(2ωx+ )+2
)+2
 =
=
 sin(4x+
sin(4x+ )+2
)+2 =
= +2kπ,k∈Z時,函數(shù)取最大值2+
+2kπ,k∈Z時,函數(shù)取最大值2+
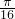 +
+ π,k∈Z}
π,k∈Z} =(cosωx,2cosωx),
=(cosωx,2cosωx), =(2cosωx,sinωx),結合函數(shù)f(x)=
=(2cosωx,sinωx),結合函數(shù)f(x)= +1和平面向量數(shù)量積公式,我們易求出函數(shù)的解析式,進而根據(jù)函數(shù)f(x)的最小正周期是
+1和平面向量數(shù)量積公式,我們易求出函數(shù)的解析式,進而根據(jù)函數(shù)f(x)的最小正周期是 ,進而求出ω的值;
,進而求出ω的值;
