
【題目】連結圓周上九個不同點的36條弦要么染成紅色,要么染成藍色,我們稱它們為“紅邊”或“藍邊”.假定由這九個點中每三個點為頂點的三角形中都含有“紅邊”.證明:這九個點中存在四個點,兩兩連結的六條邊都是紅邊.
【答案】見解析
【解析】
圓周上九個點中任三點均不共線,任四點都是一凸四邊形的頂點.設這九個點為![]() ,
,![]() ,…,
,…,![]() .顯然每個
.顯然每個![]() 都要與其他八個點有邊相連.
都要與其他八個點有邊相連.
(1)若存在一點![]() 向其他點引出至少四條藍邊,不妨設這四條藍邊為
向其他點引出至少四條藍邊,不妨設這四條藍邊為![]() ,
,![]() ,
,![]() ,
,![]() .則
.則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均為紅邊.即存在四點
均為紅邊.即存在四點![]() ,
,![]() ,
,![]() ,
,![]() ,其中每兩點連的都是紅邊(如圖).
,其中每兩點連的都是紅邊(如圖).
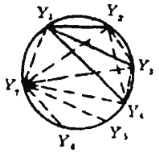
(2)若每一點向其余點引出的藍邊不多于3條.這時每兩點向其余點連的紅邊至少為5條.如果每一點都恰引出5條紅邊,則九個點恰引出![]() 條紅邊.這不可能,因為邊數必為整數.所以,必存在某個點,比如點
條紅邊.這不可能,因為邊數必為整數.所以,必存在某個點,比如點![]() ,到其他點連的紅邊至少為6條.不妨設
,到其他點連的紅邊至少為6條.不妨設![]() 與
與![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 連的
連的![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 都是紅邊,這時五條邊
都是紅邊,這時五條邊![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中至少有三條同色.不妨設
中至少有三條同色.不妨設![]() ,
,![]() ,
,![]() 同色.
同色.
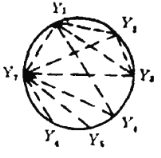
①若![]() ,
,![]() ,
,![]() 同為藍邊,因
同為藍邊,因![]() ,
,![]() ,
,![]() 均為紅邊,此時
均為紅邊,此時![]() ,
,![]() ,
,![]() ,
,![]() 四點所連六條邊均為紅邊(如圖).
四點所連六條邊均為紅邊(如圖).
②若![]() ,
,![]() ,
,![]() 同為紅邊,則
同為紅邊,則![]() 三邊依條件不能全是藍邊,即至少有一條紅邊.不妨設
三邊依條件不能全是藍邊,即至少有一條紅邊.不妨設![]() 為紅邊,這時
為紅邊,這時![]() ,
,![]() ,
,![]() ,
,![]() 四點所連的六條邊均為紅邊(如圖).
四點所連的六條邊均為紅邊(如圖).
綜上所述,問題得證.


科目:高中數學 來源: 題型:
【題目】如圖,在長方形ABCD中,AB=![]() ,AD=2,E,F為線段AB的三等分點,G、H為線段DC的三等分點.將長方形ABCD卷成以AD為母線的圓柱W的半個側面,AB、CD分別為圓柱W上、下底面的直徑.
,AD=2,E,F為線段AB的三等分點,G、H為線段DC的三等分點.將長方形ABCD卷成以AD為母線的圓柱W的半個側面,AB、CD分別為圓柱W上、下底面的直徑.

(Ⅰ)證明:平面ADHF⊥平面BCHF;
(Ⅱ)若P為DC的中點,求三棱錐H—AGP的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列有關命題的說法正確的是( )
A. 命題“若![]() ,則
,則![]() ”的否命題為:“若
”的否命題為:“若![]() 則
則![]() ”
”
B. 若![]() 為真命題,
為真命題,![]() 為假命題,則
為假命題,則![]() 均為假命題
均為假命題
C. 命題“若![]() 成等比數列,則
成等比數列,則![]() ”的逆命題為真命題
”的逆命題為真命題
D. 命題“若![]() ,則
,則![]() ”的逆否命題為真命題
”的逆否命題為真命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l方程為(m+2)x﹣(m+1)y﹣3m﹣7=0,m∈R.
(1)求證:直線l恒過定點P,并求出定點P的坐標;
(2)若直線l在x軸,y軸上的截距相等,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某企業生產的某種產品中抽取100件,測量這些產品的一項質量指標值,由測量表得如下頻數分布表:
質量指標值分組 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
頻數 | 6 | 26 | 38 | 22 | 8 |
(I)在答題卡上作出這些數據的頻率分布直方圖:
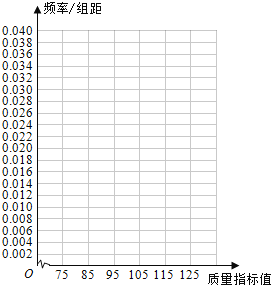
(II)估計這種產品質量指標值的平均數及方差(同一組中的數據用該組區間的中點值作代表);
(III)根據以上抽樣調查數據,能否認為該企業生產的這種產品符合“質量指標值不低于95的產品至少要占全部產品的80%”的規定?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是各項均不為
是各項均不為![]() 的等差數列,公差為
的等差數列,公差為![]() ,
,![]() 為其前
為其前![]() 項和,且滿足
項和,且滿足
![]() ,
,![]() .數列
.數列![]() 滿足
滿足![]() ,
,![]() 為數列
為數列![]() 的前n項和.
的前n項和.
(1)求![]() 、
、![]() 和
和![]() ;
;
(2)若對任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標平面上的一列點![]() 簡記為
簡記為![]() ,若由
,若由![]() 構成的數列
構成的數列![]() 滿足
滿足![]() ,(其中
,(其中![]() 是與
是與![]() 軸正方向相同的單位向量),則稱
軸正方向相同的單位向量),則稱![]() 為“
為“![]() 點列”.
點列”.
(1)試判斷:![]() ,...是否為“
,...是否為“![]() 點列”?并說明理由.
點列”?并說明理由.
(2)若![]() 為“
為“![]() 點列”,且點
點列”,且點![]() 在點
在點![]() 的右上方.任取其中連續三點
的右上方.任取其中連續三點![]() ,判斷
,判斷![]() 的形狀(銳角,直角,鈍角三角形),并證明.
的形狀(銳角,直角,鈍角三角形),并證明.
(3)若![]() 為“
為“![]() 點列”,正整數
點列”,正整數![]() 滿足:
滿足:![]() ,且
,且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com