【題目】古印度“漢諾塔問題”：一塊黃銅平板上裝著
三根金銅石細(xì)柱，其中細(xì)柱
上套著個大小不等的環(huán)形金盤，大的在下、小的在上.將這些盤子全部轉(zhuǎn)移到另一根柱子上，移動規(guī)則如下：一次只能將一個金盤從一根柱子轉(zhuǎn)移到另外一根柱子上，不允許將較大盤子放在較小盤子上面.若柱上現(xiàn)有
個金盤（如圖），將柱上的金盤全部移到
柱上，至少需要移動次數(shù)為（ ）
A.
B.
C.
D.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在極坐標(biāo)系中，直線l：
，P為直線l上一點，且點P在極軸上方
以OP為一邊作正三角形
逆時針方向
，且
面積為
．
求Q點的極坐標(biāo)；
求外接圓的極坐標(biāo)方程，并判斷直線l與外接圓的位置關(guān)系．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】十九大提出，堅決打贏脫貧攻堅戰(zhàn)，某幫扶單位為幫助定點扶貧村真脫貧，堅持扶貧同扶智相結(jié)合，幫助貧困村種植蜜柚，并利用電商進行銷售，為了更好地銷售，現(xiàn)從該村的蜜柚樹上隨機摘下了100個蜜柚進行測重，其質(zhì)量分別在
，
，
，
，
，
（單位：克）中，其頻率分布直方圖如圖所示.
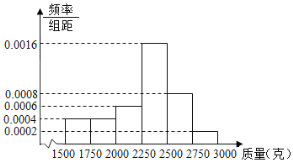
（1）按分層抽樣的方法從質(zhì)量落在，的蜜柚中抽取5個，再從這5個蜜柚中隨機抽取2個，求這2個蜜柚質(zhì)量均小于2000克的概率；
（2）以各組數(shù)據(jù)的中間數(shù)代表這組數(shù)據(jù)的平均水平，以頻率代表概率，已知該貧困村的蜜柚樹上大約還有5000個蜜柚等待出售，某電商提出兩種收購方案：
A. 所有蜜柚均以40元/千克收購；
B. 低于2250克的蜜柚以60元/個收購，高于或等于2250克的以80元/個收購.
請你通過計算為該村選擇收益最好的方案.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】2018年，依托用戶碎片化時間的娛樂需求、分享需求以及視頻態(tài)的信息負(fù)載力，短視頻快速崛起；與此同時，移動閱讀方興未艾，從側(cè)面反應(yīng)了人們對精神富足的一種追求，在習(xí)慣了大眾娛樂所帶來的短暫愉悅后，部分用戶依舊對有著傳統(tǒng)文學(xué)底蘊的嚴(yán)肅閱讀青睞有加．
某讀書APP抽樣調(diào)查了非一線城市M和一線城市N各100名用戶的日使用時長（單位：分鐘），繪制成頻率分布直方圖如下，其中日使用時長不低于60分鐘的用戶記為“活躍用戶”．
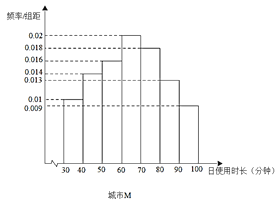
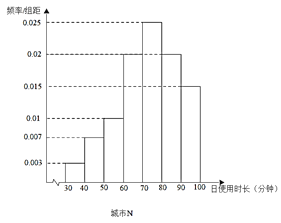
（1）請?zhí)顚懸韵?/span>
列聯(lián)表，并判斷是否有99．5%的把握認(rèn)為用戶活躍與否與所在城市有關(guān)？
活躍用戶 | 不活躍用戶 | 合計 | |
城市M | |||
城市N | |||
合計 |
（2）以頻率估計概率，從城市M中任選2名用戶，從城市N中任選1名用戶，設(shè)這3名用戶中活躍用戶的人數(shù)為
，求的分布列和數(shù)學(xué)期望．
（3）該讀書APP還統(tǒng)計了2018年4個季度的用戶使用時長y（單位：百萬小時），發(fā)現(xiàn)y與季度（
）線性相關(guān)，得到回歸直線為
，已知這4個季度的用戶平均使用時長為12.3百萬小時，試以此回歸方程估計2019年第一季度（
）該讀書APP用戶使用時長約為多少百萬小時．
附：
，其中
．
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系
中，以
為極點，
軸的正半軸為極軸，建立極坐標(biāo)系，曲線
的極坐標(biāo)方程為
；直線
的參數(shù)方程為
（
為參數(shù)），直線與曲線分別交于
，
兩點.
（1）寫出曲線的直角坐標(biāo)方程和直線的普通方程；
（2）若點
的極坐標(biāo)為
，
，求
的值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】給出下列四個命題：
①
中，
是
成立的充要條件；
②當(dāng)
時，有
；
③已知
是等差數(shù)列
的前n項和，若
，則
；
④若函數(shù)
為
上的奇函數(shù)，則函數(shù)
的圖象一定關(guān)于點
成中心對稱．其中所有正確命題的序號為___________．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某校進行了一次創(chuàng)新作文大賽，共有100名同學(xué)參賽，經(jīng)過評判，這100名參賽者的得分都在
之間，其得分的頻率分布直方圖如圖，則下列結(jié)論錯誤的是（ ）
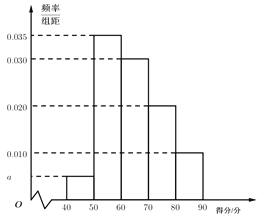
A.得分在
之間的共有40人
B.從這100名參賽者中隨機選取1人，其得分在
的概率為0.5
C.估計得分的眾數(shù)為55
D.這100名參賽者得分的中位數(shù)為65
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
：
（
）的離心率為
，且橢圓的一個焦點與拋物線
的焦點重合.過點
的直線
交橢圓于
，
兩點，
為坐標(biāo)原點.
（1）若直線過橢圓的上頂點，求
的面積；
（2）若
，
分別為橢圓的左、右頂點，直線
，
，
的斜率分別為
，
，
，求
的值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
