
【題目】設函數f(x)=|x﹣a|+|x+b|,ab>0.
(1)當a=1,b=1時,求不等式f(x)<3的解集;
(2)若f(x)的最小值為2,求![]() 的最小值.
的最小值.
【答案】(1){x|![]() }(2)
}(2)![]()
【解析】
(1)原不等式等價于|x﹣1|+|x+1|<3,然后對x分類去絕對值,化為關于x的一元一次不等式求解,取并集得答案;
(2)f(x)=|x﹣a|+|x+b|≥|b+a|,當且僅當(x﹣a)(x+b)≤0時等號成立.可得f(x)的最小值為|b+a|=2.結合ab>0,得|b+a|=|a|+|b|=2,則![]() ,展開后利用基本不等式求最值.
,展開后利用基本不等式求最值.
(1)原不等式等價于|x﹣1|+|x+1|<3,
當x≥1時,可得x﹣1+x+1<3,解得1≤x![]() ;
;
當﹣1<x<1時,可得﹣x+1+x+1<3,得2<3成立;
當x≤﹣1時,可得﹣x+1﹣x﹣1<3,解得![]() x≤﹣1.
x≤﹣1.
綜上所述,原不等式的解集為{x|![]() };
};
(2)f(x)=|x﹣a|+|x+b|≥|b+a|,當且僅當(x﹣a)(x+b)≤0時等號成立.
∴f(x)的最小值為|b+a|,即|b+a|=2.
又∵ab>0,∴|b+a|=|a|+|b|=2,
∴![]()
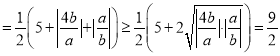 .
.
當且僅當![]() 時,等號成立,
時,等號成立,
∴![]() 的最小值為
的最小值為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,橢圓
,橢圓![]() 與
與![]() 軸交于
軸交于![]() 兩點,且
兩點,且![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設點![]() 是橢圓
是橢圓![]() 上的一個動點,且直線
上的一個動點,且直線![]() 與直線
與直線![]() 分別交于
分別交于![]() 兩點.是否存在點
兩點.是否存在點![]() 使得以
使得以![]() 為直徑的圓經過點
為直徑的圓經過點![]() ?若存在,求出點
?若存在,求出點![]() 的橫坐標;若不存在,說明理由.
的橫坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電動車生產企業,上年度生產電動車的投入成本為1萬元/輛,出廠價為1.2萬元/輛,年銷售量為1000輛.本年度為適應市場需求,計劃提高產品檔次,適度增加投入成本.若每輛車投入成本增加的比例為![]() ,則出廠價相應提高的比例為
,則出廠價相應提高的比例為![]() ,且當
,且當![]() 不超過0.5時,預計年銷售量增加的比例為
不超過0.5時,預計年銷售量增加的比例為![]() ,而當
,而當![]() 超過0.5時,預計年銷售量不變.已知年利潤=(出廠價-投入成本)×年銷售量.則本年度預計的年利潤
超過0.5時,預計年銷售量不變.已知年利潤=(出廠價-投入成本)×年銷售量.則本年度預計的年利潤![]() 與投入成本增加的比例
與投入成本增加的比例![]() 的關系式為______;為使本年度利潤比上年有所增加,投入成本增加的比例
的關系式為______;為使本年度利潤比上年有所增加,投入成本增加的比例![]() 的取值范圍為______.
的取值范圍為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,側面ABB1A1是菱形,且CA=CB1.
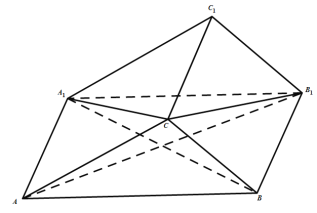
(1)證明:面CBA1⊥面CB1A;
(2)若∠BAA1=60°,A1C=BC=BA1,求二面角C﹣A1B1﹣C1的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知⊙M過點![]() ,且與⊙N:
,且與⊙N:![]() 內切,設⊙M的圓心M的軌跡為曲線C.
內切,設⊙M的圓心M的軌跡為曲線C.
(1)求曲線C的方程:
(2)設直線l不經過點![]() 且與曲線C相交于P,Q兩點.若直線PB與直線QB的斜率之積為
且與曲線C相交于P,Q兩點.若直線PB與直線QB的斜率之積為![]() ,判斷直線l是否過定點,若過定點,求出此定點坐標;若不過定點,請說明理由.
,判斷直線l是否過定點,若過定點,求出此定點坐標;若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定橢圓![]()
![]() ,稱圓心在原點
,稱圓心在原點![]() ,半徑為
,半徑為![]() 的圓是橢圓
的圓是橢圓![]() 的“準圓”.若橢圓
的“準圓”.若橢圓![]() 的一個焦點為
的一個焦點為![]() ,其短軸上的一個端點到
,其短軸上的一個端點到![]() 的距離為
的距離為![]() .
.
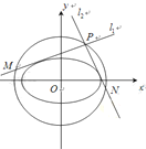
(1)求橢圓![]() 的方程和其“準圓”方程;
的方程和其“準圓”方程;
(2)點![]() 是橢圓
是橢圓![]() 的“準圓”上的動點,過點
的“準圓”上的動點,過點![]() 作橢圓的切線
作橢圓的切線![]() 交“準圓”于點
交“準圓”于點![]() .
.
①當點![]() 為“準圓”與
為“準圓”與![]() 軸正半軸的交點時,求直線
軸正半軸的交點時,求直線![]() 的方程并證明
的方程并證明![]() ;
;
②求證:線段![]() 的長為定值.
的長為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某企業近3年的前7個月的月利潤(單位:百萬元)如下面的折線圖所示:
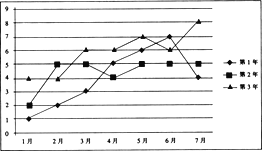
(1)試問這3年的前7個月中哪個月的月平均利潤最高?
(2)通過計算判斷這3年的前7個月的總利潤的發展趨勢;
(3)試以第3年的前4個月的數據(如下表),用線性回歸的擬合模式估測第3年8月份的利潤.
月份x | 1 | 2 | 3 | 4 |
利潤y(單位:百萬元) | 4 | 4 | 6 | 6 |
相關公式: 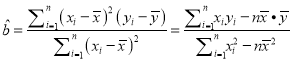 ,
, ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com