
【題目】已知函數![]() ,其中
,其中![]() .
.
(1)當![]() 時,求證:過原點
時,求證:過原點![]() 且與曲線
且與曲線![]() 相切的直線有且只有一條;
相切的直線有且只有一條;
(2)當![]() 時,不等式
時,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析(2)![]()
【解析】
(1) 根據導數的幾何意義,求出函數上任意一點![]() 處的切線方程,根據過原點知
處的切線方程,根據過原點知![]() 有唯一解即可求證;
有唯一解即可求證;
(2) 構造函數![]() ,求導后再分類討論,根據導數和函數的單調性和最值的關系即可求出a的范圍.
,求導后再分類討論,根據導數和函數的單調性和最值的關系即可求出a的范圍.
(1)函數![]() 的導函數為
的導函數為![]() .
.
曲線![]() 上任意一點
上任意一點![]() 處的切線方程為
處的切線方程為![]() .
.
此切線過原點![]() 當且僅當
當且僅當![]() ,即
,即![]() .
.
當![]() ,則方程
,則方程![]() 有且只有一個解
有且只有一個解![]() ,
,
曲線![]() 在原點
在原點![]() 處的切線
處的切線![]() 過原點
過原點![]() .
.
綜上所述,無論![]() 取什么值,過原點
取什么值,過原點![]() 且與曲線
且與曲線![]() 相切的直線都有且只有一條,即直線
相切的直線都有且只有一條,即直線![]() .
.
(2)令![]() ,
,
則![]() .
.
①若![]() ,則
,則![]() ,故
,故![]() 在
在![]() 上單調遞增.
上單調遞增.
因此,當![]() 時,
時,![]() ;
;
②若![]() ,則
,則![]() .
.
當![]() 時,
時,![]() ,
,![]() .
.
令![]() ,則
,則![]() .
.
而當![]() 時,
時,![]() ,
,![]() ,于是:
,于是:
若![]() ,則
,則![]() ,故
,故![]() 在
在![]() 上單調遞增.
上單調遞增.
因此,當![]() 時,
時,![]() ,進而
,進而![]() ,
,
故![]() 在
在![]() 上單調遞增.
上單調遞增.
因此,當![]() 時,
時,![]() ;
;
若![]() ,則存在
,則存在![]() ,使得
,使得![]() .
.
當![]() 時,
時,![]() ,
,
![]() ,故
,故![]() 在
在![]() 上單調遞減.
上單調遞減.
因此,當![]() 時,
時,![]() ,進而
,進而![]() ,
,
故![]() 在
在![]() 上單調遞減.
上單調遞減.
因此,當![]() 時,
時,![]() .
.
綜上所述,實數![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】某市政府為減輕汽車尾氣對大氣的污染,保衛藍天,鼓勵廣大市民使用電動交通工具出行,決定為電動車(含電動自行車和電動汽車)免費提供電池檢測服務.現從全市已掛牌照的![]() 電動車中隨機抽取100輛委托專業機構免費為它們進行電池性能檢測,電池性能分為需要更換、尚能使用、較好、良好四個等級,并分成電動自行車和電動汽車兩個群體分別進行統計,樣本分布如圖.
電動車中隨機抽取100輛委托專業機構免費為它們進行電池性能檢測,電池性能分為需要更換、尚能使用、較好、良好四個等級,并分成電動自行車和電動汽車兩個群體分別進行統計,樣本分布如圖.
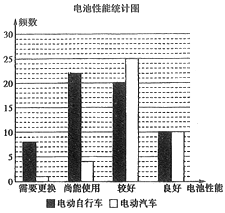
(1)采用分層抽樣的方法從電池性能較好的電動車中隨機抽取9輛,再從這9輛中隨機抽取2輛,求至少有一輛為電動汽車的概率;
(2)為進一步提高市民對電動車的使用熱情,市政府準備為電動車車主一次性發放補助,標準如下:①電動自行車每輛補助300元;②電動汽車每輛補助500元;③對電池需要更換的電動車每輛額外補助400元.試求抽取的100輛電動車執行此方案的預算;并利用樣本估計總體,試估計市政府執行此方案的預算.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著2022年北京冬奧會的臨近,中國冰雪產業快速發展,冰雪運動人數快速上升,冰雪運動市場需求得到釋放.如圖是2012-2018年中國雪場滑雪人數(單位:萬人)與同比增長情況統計圖.則下面結論中正確的是( )

①2012-2018年,中國雪場滑雪人數逐年增加;②2013-2015年,中國雪場滑雪人數和同比增長率均逐年增加;③中國雪場2015年比2014年增加的滑雪人數和2018年比2017年增加的滑雪人數均為220萬人,因此這兩年的同比增長率均有提高;④2016-2018年,中國雪場滑雪人數的增長率約為23.4%.
A.①②③B.②③④C.①②D.③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=|x﹣a|+|x+b|,ab>0.
(1)當a=1,b=1時,求不等式f(x)<3的解集;
(2)若f(x)的最小值為2,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年,全國各地區堅持穩中求進工作總基調,經濟運行總體平穩,發展水平邁上新臺階,發展質量穩步上升,人民生活福祉持續增進,全年最終消費支出對國內生產總值增長的貢獻率為57.8%.下圖為2019年居民消費價格月度漲跌幅度:(同比![]() (本期數-去年同期數)/去年同期數
(本期數-去年同期數)/去年同期數![]() ,環比
,環比![]() (本期數-上期數)/上期數
(本期數-上期數)/上期數![]()
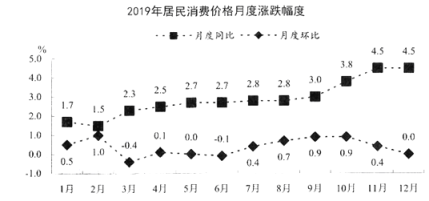
下列結論中不正確的是( )
A.2019年第三季度的居民消費價格一直都在增長
B.2018年7月份的居民消費價格比同年8月份要低一些
C.2019年全年居民消費價格比2018年漲了2.5%以上
D.2019年3月份的居民消費價格全年最低
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】上世紀末河南出土的以鶴的尺骨(翅骨)制成的“骨笛”(圖1),充分展示了我國古代高超的音律藝術及先進的數學水平,也印證了我國古代音律與歷法的密切聯系.圖2為骨笛測量“春(秋)分”,“夏(冬)至”的示意圖,圖3是某骨笛的部分測量數據(骨笛的彎曲忽略不計),夏至(或冬至)日光(當日正午太陽光線)與春秋分日光(當日正午太陽光線)的夾角等于黃赤交角.


由歷法理論知,黃赤交角近1萬年持續減小,其正切值及對應的年代如下表:
黃赤交角 |
|
|
|
|
|
正切值 | 0.439 | 0.444 | 0.450 | 0.455 | 0.461 |
年代 | 公元元年 | 公元前2000年 | 公元前4000年 | 公元前6000年 | 公元前8000年 |
根據以上信息,通過計算黃赤交角,可估計該骨笛的大致年代是( )
A.公元前2000年到公元元年B.公元前4000年到公元前2000年
C.公元前6000年到公元前4000年D.早于公元前6000年
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學長期堅持貫徹以人為本,因材施教的教育理念,每年都會在校文化節期間舉行“數學素養能力測試”和“語文素養能力測試”兩項測試,以給學生課外興趣學習及輔導提供參考依據.成績分為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五個等級(等級
五個等級(等級![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別對應5分,4分,3分,2分,1分).某班學生兩科的考試成績的數據統計如圖所示,其中“語文素養能力測試”科目的成績為
分別對應5分,4分,3分,2分,1分).某班學生兩科的考試成績的數據統計如圖所示,其中“語文素養能力測試”科目的成績為![]() 的考生有3人.
的考生有3人.
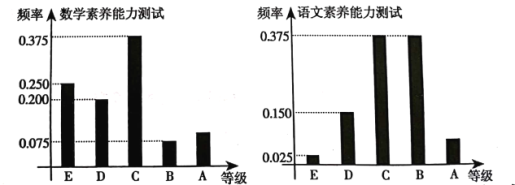
(1)求該班“數學素養能力測試”的科目平均分以及“數學素養能力測試”科目成績為![]() 的人數;
的人數;
(2)若該班共有9人得分大于7分,其中有2人10分,3人9分,4人8分.從這9人中隨機抽取三人,設三人的成績之和為![]() ,求
,求![]() .
.
(3)從該班得分大于7分的9人中選3人即甲,乙,丙組隊參加學校內的“數學限時解題挑戰賽”.規則為:每隊首先派一名隊員參加挑戰賽,在限定的時間,若該生解決問題,即團隊挑戰成功,結束挑戰;若解決問題失敗,則派另外一名隊員上去挑戰,直至派完隊員為止.通過訓練,已知甲,乙,丙通過挑戰賽的概率分別是![]() ,
,![]() ,
,![]() ,問以怎樣的先后順序派出隊員,可使得派出隊員數目的均值達到最小?(只需寫出結果)
,問以怎樣的先后順序派出隊員,可使得派出隊員數目的均值達到最小?(只需寫出結果)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的標準方程是
的標準方程是![]() ,設
,設![]() 是橢圓
是橢圓![]() 的左焦點,
的左焦點,![]() 為直線
為直線![]() 上任意一點,過
上任意一點,過![]() 做
做![]() 的垂線交橢圓
的垂線交橢圓![]() 于點
于點![]() ,
,![]() .
.
(1)證明:線段![]() 平分線段
平分線段![]() (其中
(其中![]() 為坐標原點);
為坐標原點);
(2)當![]() 最小時,求點
最小時,求點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com