
分析 根據函數g(x)的解析式求出g′(x)和g″(x),令g″(x)=0,求得x的值,由此求得三次函數g(x)的對稱中心.由于函數的對稱中心為(1,4),可知g(x)+f(2-x)=8,由此能夠求出所給的式子的值.
解答 解:由g(x)=x3-3x2+4x+2,
得:g′(x)=3x2-6x+4,g″(x)=6x-6,
令g″(x)=0,解得:x=1,
∴函數g(x)的對稱中心是(1,4),
∴g(2-x)+g(x)=8,
故設$g(\frac{1}{10})+g(\frac{2}{10})+g(\frac{3}{10})+…+g(\frac{19}{10})$=m,
則g($\frac{19}{10}$)+g($\frac{18}{10}$)+g($\frac{17}{10}$)+…+g($\frac{1}{10}$)=m,
兩式相加得:8×19=2m,解得:m=76,
故答案為:76.
點評 本小題主要考查函數與導數等知識,考查化歸與轉化的數學思想方法,考查化簡計算能力,求函數的值以及函數的對稱性的應用,屬于中檔題.


科目:高中數學 來源: 題型:解答題
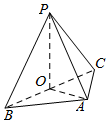 如圖,在三棱錐P-ABC中,△PAB和△PAC均為邊長是$\sqrt{2}$的正三角形,且∠BAC=90°,O為BC的中點.
如圖,在三棱錐P-ABC中,△PAB和△PAC均為邊長是$\sqrt{2}$的正三角形,且∠BAC=90°,O為BC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 80 m | B. | 20 m | C. | 40 m | D. | 50 m |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | a |
| A. | 3 | B. | 3.15 | C. | 3.5 | D. | 4.5 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com