
【題目】已知![]() 為等邊三角形,
為等邊三角形,![]() ,P,Q依次為AC,AB上的點,且線段PQ將
,P,Q依次為AC,AB上的點,且線段PQ將![]() 分為面積相等的兩部分,設
分為面積相等的兩部分,設![]() ,
,![]() ,
,![]() .
.
(1)用解析式將t表示成x的函數;
(2)用解析式將y表示成x的函數;
(3)求y的最大值與最小值.
科目:高中數學 來源: 題型:
【題目】設函數![]() ,
,![]() ,
,![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)若![]() (其中
(其中![]() ),證明:
),證明:![]() ;
;
(3)是否存在實數a,使得![]() 在區間
在區間![]() 內恒成立,且關于x的方程
內恒成立,且關于x的方程![]() 在
在![]() 內有唯一解?請說明理由.
內有唯一解?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為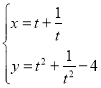 (
(![]() 為參數).
為參數).
(1)求曲線![]() 的普通方程;
的普通方程;
(2)以![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,直線
軸的非負半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() ,(
,(![]() ),直線
),直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,求線段
兩點,求線段![]() 的長度
的長度![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,幾何體是圓柱的一部分,它是由矩形ABCD(及其內部)以AB邊所在直線為旋轉軸旋轉120°得到的,G是![]() 的中點.
的中點.

(1)設P是![]() 上的一點,且AP⊥BE,求∠CBP的大小;
上的一點,且AP⊥BE,求∠CBP的大小;
(2)當AB=3,AD=2時,求二面角E-AG-C的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
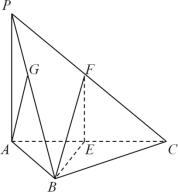
【題目】如圖,三棱錐![]() 中,底面△
中,底面△![]() 是邊長為2的正三角形,
是邊長為2的正三角形,![]() ,
,![]() 底面
底面![]() ,點
,點![]() 分別為
分別為![]() ,
,![]() 的中點.
的中點.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在點
上是否存在點![]() ,使得三棱錐
,使得三棱錐![]() 體積為
體積為![]() ?若存在,確定點
?若存在,確定點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知甲盒內有大小相同的1個紅球和3個黑球,乙盒內有大小相同的2個紅球和4個黑球,現從甲、乙兩個盒內各任取2個球.
(1)求取出的4個球均為黑球的概率.
(2)求取出的4個球中恰有1個紅球的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】家具公司制作木質的書桌和椅子,需要木工和漆工兩道工序,已知木工平均四個小時做一把椅子,八個小時做一張書桌,該公司每星期木工最多有8000個工作時;漆工平均兩小時漆一把椅子、一小時漆一張書桌,該公司每星期漆工最多有1300個工作時,又已知制作一把椅子和一張書桌的利潤分別是15元和20元,試根據以上條件,問怎樣安排生產能獲得最大利潤?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若有平面![]() 與
與![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,則下列命題中真命題的序號有________.(1)過點
,則下列命題中真命題的序號有________.(1)過點![]() 且垂直于
且垂直于![]() 的直線平行于
的直線平行于![]() ;(2)過點
;(2)過點![]() 且垂直于
且垂直于![]() 的平面垂直于
的平面垂直于![]() ;(3)過點
;(3)過點![]() 且垂直于
且垂直于![]() 的直線在
的直線在![]() 內;(4)過點
內;(4)過點![]() 且垂直于
且垂直于![]() 的直線在
的直線在![]() 內.
內.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com