
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為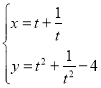 (
(![]() 為參數).
為參數).
(1)求曲線![]() 的普通方程;
的普通方程;
(2)以![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,直線
軸的非負半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() ,(
,(![]() ),直線
),直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,求線段
兩點,求線段![]() 的長度
的長度![]() .
.
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,曲線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]()
(1)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() ,點
,點![]() 為曲線
為曲線![]() 上的動點,求線段
上的動點,求線段![]() 的中點
的中點![]() 到直線
到直線![]() 的距離的最大值.并求此時點
的距離的最大值.并求此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】阿波羅尼斯(古希臘數學家,約公元前262-190年)的著作《圓錐曲線論》是古代世界光輝的科學成果,它將圓錐曲線的性質網羅殆盡,幾乎使后人沒有插足的余地.他證明過這樣一個命題:平面內與兩定點距離的比為常數![]() 的點的軌跡是圓,后人將這個圓稱為阿波羅尼斯圓.①若定點為
的點的軌跡是圓,后人將這個圓稱為阿波羅尼斯圓.①若定點為![]() ,寫出
,寫出![]() 的一個阿波羅尼斯圓的標準方程__________;②△
的一個阿波羅尼斯圓的標準方程__________;②△![]() 中,
中,![]() ,則當△
,則當△![]() 面積的最大值為
面積的最大值為![]() 時,
時,![]() ______.
______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線l的參數方程為
中,直線l的參數方程為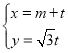 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的普通方程和C的直角坐標方程;
的普通方程和C的直角坐標方程;
(2)直線![]() 上的點
上的點![]() 為曲線
為曲線![]() 內的點,且直線
內的點,且直線![]() 與曲線
與曲線![]() 交于
交于![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直四棱柱![]() 中,底面
中,底面![]() 是邊長為6的正方形,點
是邊長為6的正方形,點![]() 在線段
在線段![]() 上,且滿足
上,且滿足![]() ,過點
,過點![]() 作直四棱柱
作直四棱柱![]() 外接球的截面,所得的截面面積的最大值與最小值之差為
外接球的截面,所得的截面面積的最大值與最小值之差為![]() ,則直四棱柱
,則直四棱柱![]() 外接球的半徑為( )
外接球的半徑為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
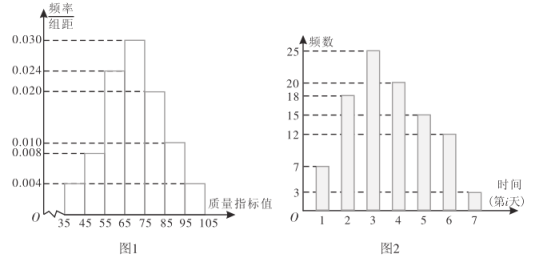
【題目】某工廠的一臺某型號機器有2種工作狀態:正常狀態和故障狀態.若機器處于故障狀態,則停機檢修.為了檢查機器工作狀態是否正常,工廠隨機統計了該機器以往正常工作狀態下生產的1000個產品的質量指標值,得出如圖1所示頻率分布直方圖.由統計結果可以認為,這種產品的質量指標值服從正態分布![]() ,其中
,其中![]() 近似為這1000個產品的質量指標值的平均數
近似為這1000個產品的質量指標值的平均數![]() ,
,![]() 近似為這1000個產品的質量指標值的方差
近似為這1000個產品的質量指標值的方差![]() (同一組中的數據用該組區間中點值為代表).若產品的質量指標值全部在
(同一組中的數據用該組區間中點值為代表).若產品的質量指標值全部在![]() 之內,就認為機器處于正常狀態,否則,認為機器處于故障狀態.
之內,就認為機器處于正常狀態,否則,認為機器處于故障狀態.
(1)下面是檢驗員在一天內從該機器生產的產品中隨機抽取10件測得的質量指標值:
29 45 55 63 67 73 78 87 93 113
請判斷該機器是否出現故障?
(2)若機器出現故障,有2種檢修方案可供選擇:
方案一:加急檢修,檢修公司會在當天排除故障,費用為700元;
方案二:常規檢修,檢修公司會在七天內的任意一天來排除故障,費用為200元.
現需決策在機器出現故障時,該工廠選擇何種方案進行檢修,為此搜集檢修公司對該型號機器近100單常規檢修在第i(![]() ,2,…,7)天檢修的單數,得到如圖2所示柱狀圖,將第i天常規檢修單數的頻率代替概率.已知該機器正常工作一天可收益200元,故障機器檢修當天不工作,若機器出現故障,該選擇哪種檢修方案?
,2,…,7)天檢修的單數,得到如圖2所示柱狀圖,將第i天常規檢修單數的頻率代替概率.已知該機器正常工作一天可收益200元,故障機器檢修當天不工作,若機器出現故障,該選擇哪種檢修方案?
附:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() (
(![]() )上的兩個動點
)上的兩個動點![]() 和
和![]() ,焦點為F.線段AB的中點為
,焦點為F.線段AB的中點為![]() ,且A,B兩點到拋物線的焦點F的距離之和為8.
,且A,B兩點到拋物線的焦點F的距離之和為8.
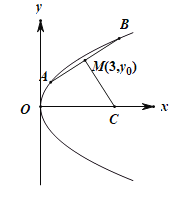
(1)求拋物線的標準方程;
(2)若線段AB的垂直平分線與x軸交于點C,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為等邊三角形,
為等邊三角形,![]() ,P,Q依次為AC,AB上的點,且線段PQ將
,P,Q依次為AC,AB上的點,且線段PQ將![]() 分為面積相等的兩部分,設
分為面積相等的兩部分,設![]() ,
,![]() ,
,![]() .
.
(1)用解析式將t表示成x的函數;
(2)用解析式將y表示成x的函數;
(3)求y的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】著名數學家華羅庚先生曾說過:“數缺形時少直觀,形缺數時難入微數形結合百般好,隔裂分家萬事休.”在數學的學習和研究中,我們經常用函數的圖象來研究函數的性質,也經常用函數的解析式來琢磨函數的圖象的特征,如某體育品牌的LOGO為![]() ,可抽象為如圖所示的軸對稱的優美曲線,下列函數中,其圖象大致可“完美”局部表達這條曲線的函數是( )
,可抽象為如圖所示的軸對稱的優美曲線,下列函數中,其圖象大致可“完美”局部表達這條曲線的函數是( )
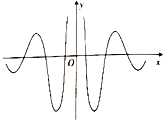
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com