
【題目】關于不同的直線![]() 與不同的平面
與不同的平面![]() ,有下列六個命題:
,有下列六個命題:
①若![]() 則
則![]() ;
;
②若![]() 則
則![]() ;
;
③若![]() 且
且![]() 則
則![]() ;
;
④若![]() 且
且![]() 則
則![]() ;
;
⑤若![]() 且
且![]() 則
則![]() ;
;
⑥若![]() 且
且![]() 則
則![]() ;
;
其中正確命題的序號是__________;
【答案】①③⑤
【解析】
①:根據線面平行的性質定理、面面垂直的判定定理,結合平行線的性質進行判斷即可;
②:根據線面平行的判定定理進行判斷即可;
③:根據線面平行的性質定理、面面平行的性質,以及平行線的性質進行判斷即可;
④:在正方體中可以找到特例進行判斷即可;
⑤:根據平面法向量的性質和空間向量夾角公式進行判斷即可;
⑥:根據面面平行的性質,結合直線與直線的位置關系進行判斷即可.
①:因為![]() ,所以存在過直線
,所以存在過直線![]() 的一個平面與平面
的一個平面與平面![]() 交于直線
交于直線![]() ,顯然有
,顯然有![]() ,而
,而![]() ,所以
,所以![]() ,而
,而![]() ,因此
,因此![]() ,故本命題是真命題;
,故本命題是真命題;
②:只有當![]() ,
,![]() 才能推出
才能推出![]() ,故本命題是假命題;
,故本命題是假命題;
③:因為![]() ,所以存在過直線
,所以存在過直線![]() 的一個平面與平面
的一個平面與平面![]() 交于直線
交于直線![]() ,顯然有
,顯然有![]() ,又
,又![]() ,所以
,所以![]() ,因此
,因此![]() ,所以
,所以![]() ,故本命題是真命題;
,故本命題是真命題;
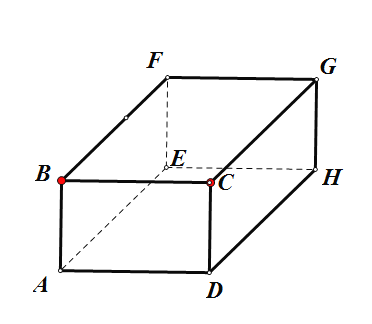
④:在如圖的正方體![]() 中:
中:
平面![]() 記為平面
記為平面![]() ,平面
,平面![]() 記為平面
記為平面![]() ,直線
,直線![]() 記為直線
記為直線![]() ,直線
,直線![]() 記為直線
記為直線![]() ,顯然符合
,顯然符合![]()
![]() ,但是
,但是![]() ,(當然
,(當然![]() 也可以是異面直線),故本命題是假命題,
也可以是異面直線),故本命題是假命題,
⑤:因為![]() ,所以平面
,所以平面![]() 的法向量分別為:
的法向量分別為:![]() ,因為
,因為![]() 所以為
所以為![]() ,故本命題是真命題;
,故本命題是真命題;
⑥:因為![]() 且
且![]() 所以直線
所以直線![]() 沒有交點,故兩直線是平行線或異面直線,故本命題是假命題.
沒有交點,故兩直線是平行線或異面直線,故本命題是假命題.
故答案為:①③⑤


科目:高中數學 來源: 題型:
【題目】十九大提出,堅決打贏脫貧攻堅戰,某幫扶單位為幫助定點扶貧村真脫貧,堅持扶貧同扶智相結合,幫助貧困村種植蜜柚,并利用電商進行銷售,為了更好地銷售,現從該村的蜜柚樹上隨機摘下了![]() 個蜜柚進行測重,其質量分別在
個蜜柚進行測重,其質量分別在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() (單位:克)中,其頻率分布直方圖如圖所示,
(單位:克)中,其頻率分布直方圖如圖所示,

(Ⅰ)已經按分層抽樣的方法從質量落在![]() ,
,![]() 的蜜柚中抽取了
的蜜柚中抽取了![]() 個,現從這
個,現從這![]() 個蜜柚中隨機抽取
個蜜柚中隨機抽取![]() 個。求這
個。求這![]() 個蜜柚質量均小于
個蜜柚質量均小于![]() 克的概率:
克的概率:
(Ⅱ)以各組數據的中間值代表這組數據的平均水平,以頻率代表概率,已知該貧困村的蜜柚樹上大約還有![]() 個蜜柚等待出售,某電商提出了兩種收購方案:
個蜜柚等待出售,某電商提出了兩種收購方案:
方案一:所有蜜柚均以![]() 元/千克收購;
元/千克收購;
方案二:低于![]() 克的蜜柚以
克的蜜柚以![]() 元/個收購,高于或等于
元/個收購,高于或等于![]() 克的以
克的以![]() 元/個收購.
元/個收購.
請你通過計算為該村選擇收益最好的方案.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一汽車廠生產![]() 三類轎車,每類轎車均有舒適型和標準型兩種型號,某月的產量如表(單位:輛):
三類轎車,每類轎車均有舒適型和標準型兩種型號,某月的產量如表(單位:輛):
轎車 | 轎車 | 轎車 | |
舒適型 | 100 | 150 |
|
標準型 | 300 | 450 | 600 |
按分層抽樣的方法在這個月生產的轎車中抽取50輛,其中有![]() 類轎車10輛.
類轎車10輛.
(1)求![]() 的值;
的值;
(2)用隨機抽樣的方法從![]() 類舒適型轎車中抽取8輛,經檢測它們的得分如下:4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,把這8輛轎車的得分看作一個總體,從中任取一個數,求該數與樣本平均數之差的絕對值不超過0.5的概率.
類舒適型轎車中抽取8輛,經檢測它們的得分如下:4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,把這8輛轎車的得分看作一個總體,從中任取一個數,求該數與樣本平均數之差的絕對值不超過0.5的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圓錐![]() (其中
(其中![]() 為頂點,
為頂點,![]() 為底面圓心)的側面積與底面積的比是
為底面圓心)的側面積與底面積的比是![]() ,則圓錐
,則圓錐![]() 與它的外接球(即頂點在球面上且底面圓周也在球面上)的體積比為__________.
與它的外接球(即頂點在球面上且底面圓周也在球面上)的體積比為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在單位正方體![]() 中,點
中,點![]() 在線段
在線段![]() 上運動,給出以下三個命題:
上運動,給出以下三個命題:
①三棱錐![]() 的體積為定值; ②二面角
的體積為定值; ②二面角![]() 的大小為定值;
的大小為定值;
③異面直線![]() 與直線
與直線![]() 所成的角為定值;
所成的角為定值;
其中真命題有( )
A.0個B.1個C.2個D.3個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:極坐標與參數方程]
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 是參數),以坐標原點
是參數),以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若射線![]()
![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,與曲線
兩點,與曲線![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 取最大值時
取最大值時![]() 的值
的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】時值金秋十月,正是秋高氣爽,陽光明媚的美好時刻。復興中學一年一度的校運會正在密鑼緊鼓地籌備中,同學們也在熱切地期盼著,都想為校運會出一份力。小智同學則通過對學校有關部門的走訪,隨機地統計了過去許多年中的五個年份的校運會“參與”人數及相關數據,并進行分析,希望能為運動會組織者科學地安排提供參考。
附:①過去許多年來學校的學生數基本上穩定在3500人左右;②“參與”人數是指運動員和志愿者,其余同學均為“啦啦隊員”,不計入其中;③用數字1、2、3、4、5表示小智同學統計的五個年份的年份數,今年的年份數是6;
統計表(一)
年份數x | 1 | 2 | 3 | 4 | 5 |
“參與”人數(y千人) | 1.9 | 2.3 | 2.0 | 2.5 | 2.8 |
統計表(二)
高一(3)(4)班參加羽毛球比賽的情況:
男生 | 女生 | 小計 | |
參加(人數) | 26 | b | 50 |
不參加(人數) | c | 20 | |
小計 | 44 | 100 |
(1)請你與小智同學一起根據統計表(一)所給的數據,求出“參與”人數y關于年份數x的線性回歸方程![]() ,并預估今年的校運會的“參與”人數;
,并預估今年的校運會的“參與”人數;
(2)學校命名“參與”人數占總人數的百分之八十及以上的年份為“體育活躍年”.如果該校每屆校運會的“參與”人數是互不影響的,且假定小智同學對今年校運會的“參與”人數的預估是正確的,并以這6個年份中的“體育活躍年”所占的比例作為任意一年是“體育活躍年”的概率。現從過去許多年中隨機抽取9年來研究,記這9年中“體活躍年”的個數為隨機變量![]() ,試求隨機變量
,試求隨機變量![]() 的分布列、期望
的分布列、期望![]() 和方差
和方差![]() ;
;
(3)根據統計表(二),請問:你能否有超過60%的把握認為“羽毛球運動”與“性別”有關?
參考公式和數據一: ,
,![]() ,
,![]() ,
,![]()
參考公式二: ,其中
,其中![]() .
.
參考數據:
| 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線![]() :
:![]() ,(
,(![]() 為參數),將曲線
為參數),將曲線![]() 上的所有點的橫坐標縮短為原來的
上的所有點的橫坐標縮短為原來的![]() ,縱坐標縮短為原來的
,縱坐標縮短為原來的![]() 后得到曲線
后得到曲線![]() ,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為
,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為 。
。
(1)求曲線![]() 的極坐標方程和直線l的直角坐標方程;
的極坐標方程和直線l的直角坐標方程;
(2)設直線l與曲線![]() 交于不同的兩點A,B,點M為拋物線
交于不同的兩點A,B,點M為拋物線![]() 的焦點,求
的焦點,求![]() 的值。
的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com