
【題目】四棱錐![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 為菱形,且有
為菱形,且有![]() ,
,![]() ,
,![]() 是線段
是線段![]() 上一點(diǎn),且
上一點(diǎn),且![]() 與
與![]() 所成角的正弦值是
所成角的正弦值是![]() .
.
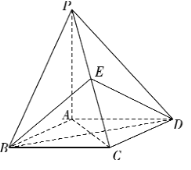
(1)求![]() 的大小;
的大小;
(2)若![]() 與平面
與平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)記![]() 與
與![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,
,![]() 的中點(diǎn)為
的中點(diǎn)為![]() ,連結(jié)
,連結(jié)![]() ,
,![]() 與
與![]() 所成的角就是
所成的角就是![]() 與
與![]() 所成的角,解
所成的角,解![]() 即可;
即可;
(2)取![]() 的中點(diǎn)
的中點(diǎn)![]() ,易得
,易得![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,在平面
,在平面![]() 內(nèi)作
內(nèi)作![]() ,則
,則![]() 平面
平面![]() ,故
,故![]() 與平面
與平面![]() 所成的角的正弦值
所成的角的正弦值![]() ,設(shè)
,設(shè)![]() ,再分別求出
,再分別求出![]() 代入即可.
代入即可.
(1)記![]() 與
與![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,
,![]() 的中點(diǎn)為
的中點(diǎn)為![]() ,連結(jié)
,連結(jié)![]() ,∴
,∴![]() ,
,
∴![]() 與
與![]() 所成的角就是
所成的角就是![]() 與
與![]() 所成的角,
所成的角,
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,![]() ,
,
∵![]() 中,
中,![]() ,
,
∴![]() (舍
(舍![]() ),
),
∴![]() ,∴
,∴![]() ,
,
又![]() 是菱形,∴
是菱形,∴![]() ;
;
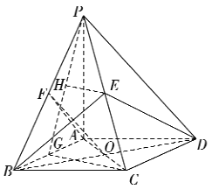
(2)取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連結(jié)
,連結(jié)![]() ,∵
,∵![]() 為正三角形,∴
為正三角形,∴![]() ,且
,且![]() ,
,
又∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,交線為
,交線為![]() ,
,
∴![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,交線為
,交線為![]() ,
,
在平面![]() 內(nèi)作
內(nèi)作![]() ,則
,則![]() 平面
平面![]() ,
,
∴![]() 與平面
與平面![]() 所成的角的正弦值
所成的角的正弦值![]() ,
,
設(shè)![]() ,則
,則![]() ,∴
,∴![]() ,且
,且![]() ,則
,則![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴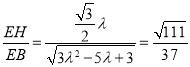 ,解得
,解得![]() (舍去
(舍去![]() ),
),
所以若![]() 與平面
與平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() ,
,![]() .
.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點(diǎn)睛新教材全能解讀系列答案
點(diǎn)睛新教材全能解讀系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,![]() 是以
是以![]() 為直徑的半圓上異于點(diǎn)
為直徑的半圓上異于點(diǎn)![]() 的點(diǎn),矩形
的點(diǎn),矩形![]() 所在的平面垂直于該半圓所在平面,且
所在的平面垂直于該半圓所在平面,且![]()
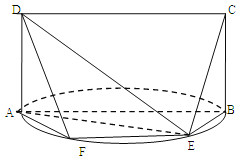
(Ⅰ)求證:![]() ;
;
(Ⅱ)設(shè)平面![]() 與半圓弧的另一個(gè)交點(diǎn)為
與半圓弧的另一個(gè)交點(diǎn)為![]() ,
,
①求證:![]() //
//![]() ;
;
②若![]() ,求三棱錐E-ADF的體積.
,求三棱錐E-ADF的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在心理學(xué)研究中,常采用對(duì)比試驗(yàn)的方法評(píng)價(jià)不同心理暗示對(duì)人的影響,具體方法如下:將參加試驗(yàn)的志愿者隨機(jī)分成兩組,一組接受甲種心理暗示,另一組接受乙種心理暗示,通過(guò)對(duì)比這兩組志愿者接受心理暗示后的結(jié)果來(lái)評(píng)價(jià)兩種心理暗示的作用.現(xiàn)有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,從中隨機(jī)抽取5人接受甲種心理暗示,另5人接受乙種心理暗示.
(1)求接受甲種心理暗示的志愿者中包含A1但不包含B1的概率;
(2)用X表示接受乙種心理暗示的女志愿者人數(shù),求X的分布列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】變量X與Y相對(duì)應(yīng)的一組數(shù)據(jù)為(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);變量U與V相對(duì)應(yīng)的一組數(shù)據(jù)為(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).r1表示變量Y與X之間的線性相關(guān)系數(shù),r2表示變量V與U之間的線性相關(guān)系數(shù),則
A. r2<r1<0 B. r2<0<r1 C. 0<r2<r1 D. r2=r1
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】有三張形狀、大小、質(zhì)地完全一致的卡片,在每張卡片上寫(xiě)上0,1,2,現(xiàn)從中任意抽取一張,將其上數(shù)字記作x,然后放回,再抽取一張,其上數(shù)字記作y,令![]() .求:
.求:
(1)![]() 所取各值的分布列;
所取各值的分布列;
(2)隨機(jī)變量![]() 的數(shù)學(xué)期望與方差.
的數(shù)學(xué)期望與方差.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求
時(shí),求![]() 在
在![]() 上的最小值;
上的最小值;
(2)若![]() 是
是![]() 的兩個(gè)不同的極值點(diǎn),且
的兩個(gè)不同的極值點(diǎn),且![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,已知直線
中,已知直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)
為參數(shù)),以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸的非負(fù)半軸為極軸建立極坐標(biāo)系,曲線
軸的非負(fù)半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)點(diǎn)![]() ,直線
,直線![]() 與曲線
與曲線![]() 的交點(diǎn)為
的交點(diǎn)為![]() 、
、![]() ,求
,求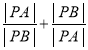 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】我國(guó)著名數(shù)學(xué)家陳景潤(rùn)在哥德巴赫猜想的研究中取得了世界矚目的成就,哥德巴赫猜想內(nèi)容是“每個(gè)大于![]() 的偶數(shù)可以表示為兩個(gè)素?cái)?shù)的和”( 注:如果一個(gè)大于
的偶數(shù)可以表示為兩個(gè)素?cái)?shù)的和”( 注:如果一個(gè)大于![]() 的整數(shù)除了
的整數(shù)除了![]() 和自身外無(wú)其他正因數(shù),則稱(chēng)這個(gè)整數(shù)為素?cái)?shù)),在不超過(guò)
和自身外無(wú)其他正因數(shù),則稱(chēng)這個(gè)整數(shù)為素?cái)?shù)),在不超過(guò)![]() 的素?cái)?shù)中,隨機(jī)選取
的素?cái)?shù)中,隨機(jī)選取![]() 個(gè)不同的素?cái)?shù)
個(gè)不同的素?cái)?shù)![]() 、
、![]() ,則
,則![]() 的概率是( )
的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() 時(shí),直線
時(shí),直線![]() 與函數(shù)
與函數(shù)![]() 圖象有三個(gè)相異的交點(diǎn),求實(shí)數(shù)
圖象有三個(gè)相異的交點(diǎn),求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)討論![]() 的單調(diào)性.
的單調(diào)性.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com