【題目】我國著名數學家陳景潤在哥德巴赫猜想的研究中取得了世界矚目的成就，哥德巴赫猜想內容是“每個大于
的偶數可以表示為兩個素數的和”（ 注：如果一個大于
的整數除了和自身外無其他正因數，則稱這個整數為素數），在不超過
的素數中，隨機選取個不同的素數
、
，則
的概率是（ ）
A.
B.
C.
D.
科目：高中數學 來源： 題型：
【題目】已知動圓經過定點
，且與定直線
相切．
（1）求動圓圓心
的軌跡方程
；
（2）已知點
，過點
作直線
與交于
，
兩點，過點作
軸的垂線分別與直線
，
交于點
，
（
為原點），求證：為線段
中點．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校為擔任班主任的教師辦理手機語音月卡套餐，為了解通話時長，采用隨機抽樣的方法，得到該校100位班主任每人的月平均通話時長
（單位：分鐘）的數據，其頻率分布直方圖如圖所示，將頻率視為概率.
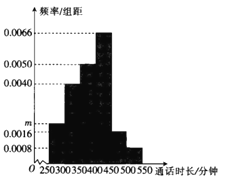
（1）求圖中
的值；
（2）估計該校擔任班主任的教師月平均通話時長的中位數；
（3）在
，
這兩組中采用分層抽樣的方法抽取6人，再從這6人中隨機抽取2人，求抽取的2人恰在同一組的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
，上、下頂點分別是
、
，上、下焦點分別是
、
，焦距為
，點
在橢圓上.
（1）求橢圓的方程；
（2）若
為橢圓上異于、的動點，過作與
軸平行的直線
，直線
與交于點
，直線
與直線
交于點
，判斷
是否為定值，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】橢圓的中心在原點，其左焦點
與拋物線
的焦點重合，過的直線
與橢圓交于
、
兩點，與拋物線交于
、
兩點．當直線與
軸垂直時，
．
（1）求橢圓的方程；
（2）求
的最大值和最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設復數β=x+yi（x，y∈R）與復平面上點P（x，y）對應．
（1）若β是關于t的一元二次方程t2﹣2t+m=0（m∈R）的一個虛根，且|β|=2，求實數m的值；
（2）設復數β滿足條件|β+3|+（﹣1）n|β﹣3|=3a+（﹣1）na（其中n∈N*、常數
），當n為奇數時，動點P（x、y）的軌跡為C1．當n為偶數時，動點P（x、y）的軌跡為C2．且兩條曲線都經過點
，求軌跡C1與C2的方程；
（3）在（2）的條件下，軌跡C2上存在點A，使點A與點B（x0，0）（x0＞0）的最小距離不小于
，求實數x0的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
