Question

已知數列{a_n}的前n項和為S_n，若S₁=1，S₂=2，且S_n+1-3S_n+2S_n-1=0（n∈N^*且n≥2），求該數列的通項公式．

Answer 1

【答案】分析：求的是數列的通項公式條件是數列{a_n}的前n項和為S_n，由所以由兩者間的關系求解．要注意分類討論．
解答：解：由S₁=1得a₁=1，又由S₂=2可知a₂=1．
∵S_n+1-3S_n+2S_n-1=0（n∈N^*且n≥2），
∴S_n+1-S_n-2S_n+2S_n-1=0（n∈N^*且n≥2），
即（S_n+1-S_n）-2（S_n-S_n-1）=0（n∈N^*且n≥2），
∴a_n+1=2a_n（n∈N^*且n≥2），故數列{a_n}從第2項起是以2為公比的等比數列．
∴數列{a_n}的通項公式為a_n=
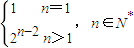點評：本題主要考查數列的前n項和通項公式及兩者間的關系的應用．