
分析 (1)首先求出函數的定義域,把a=1代入函數解析式后,求出函數的導函數,由導函數等于0求出函數的極值點,結合定義域可得函數在定義域內取得最值的情況,從而求出函數的最值.
(2)把原函數求導后,對參數a進行分類,根據a的不同取值得到導函數在不同區間內的符號,從而得到原函數的單調區間.
解答 解:(1)函數f(x)=x2-ax-aln(x-1)(a∈R)的定義域是(1,+∞)
當a=1時,f(x)=x2-x-ln(x-1),
f′(x)=2x-1-$\frac{1}{x-1}$=$\frac{2x(x-\frac{3}{2})}{x-1}$,
當x∈(1,$\frac{3}{2}$)時,f′(x)<0,
所以f (x)在(1,$\frac{3}{2}$)為減函數.
當x∈($\frac{3}{2}$,+∞)時,f′(x)>0,
所以f (x)在($\frac{3}{2}$,+∞)為增函數,
則當x=$\frac{3}{2}$時,f(x)有極小值,也就是最小值.
所以函數f (x)的最小值為f($\frac{3}{2}$)=$\frac{3}{4}$+ln2;
(2)f′(x)=2x-a-$\frac{a}{x-1}$=$\frac{2x(x-\frac{a+2}{2})}{x-1}$,
若a≤0時,則 $\frac{a+2}{2}$≤1,f′(x)>0在(1,+∞)恒成立,
所以f(x)的增區間為(1,+∞).
若a>0,則 $\frac{a+2}{2}$>1,故當x∈(1,$\frac{a+2}{2}$],f′(x)≤0,
當x∈[$\frac{a+2}{2}$,+∞)時,f′(x)≥0,
所以a>0時f(x)的減區間為(1,$\frac{a+2}{2}$],f(x)的增區間為[$\frac{a+2}{2}$,+∞).
點評 本題考查了利用導數研究函數的最值,求函數在閉區間[a,b]上的最大值與最小值是通過比較函數在(a,b)內所有極值與端點函數f(a),f(b) 比較而得到的.考查了利用導數研究函數的單調性,函數的導函數在(a,b)內恒大于等于0,原函數在該區間內單調遞增,函數的導函數在(a,b)內恒小于等于0,原函數在該區間內單調遞減,此題是中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
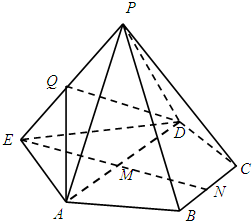 已知ABCD為等腰梯形,AD∥BC,AD=2,M,N分別為AD,BC的中點,MN=$\sqrt{3}$,現以AD為邊,作兩個正三角形△EAD與△PAD,如圖,其中平面EAD與平面ABCD共面,平面PAD⊥平面ABCD,Q為PE
已知ABCD為等腰梯形,AD∥BC,AD=2,M,N分別為AD,BC的中點,MN=$\sqrt{3}$,現以AD為邊,作兩個正三角形△EAD與△PAD,如圖,其中平面EAD與平面ABCD共面,平面PAD⊥平面ABCD,Q為PE查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
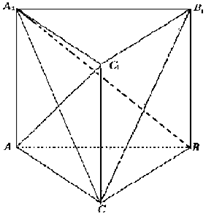 如圖,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC=3,BC=4,AB=5,AA1=3
如圖,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC=3,BC=4,AB=5,AA1=3查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com