
【題目】南航集團與波音公司2018年2月在廣州簽署協議,雙方合作的客改貨項目落戶廣州空港經濟區.根據協議,雙方將在維修技術轉讓、支持項目、管理培訓等方面開展戰略合作.現組織者對招募的100名服務志愿者培訓后,組織一次知識競賽,將所得成績制成如下頻率分布直方圖(假定每個分數段內的成績均勻分布),組織者計劃對成績前20名的參賽者進行獎勵.

(1)試求受獎勵的分數線;
(2)從受獎勵的20人中利用分層抽樣抽取5人,再從抽取的5人中抽取2人在主會場服務,試求2人成績都在90分以上(含90分)的概率.
【答案】(1) ![]() .
.
(2) ![]() .
.
【解析】分析:(Ⅰ)由頻率分布直方圖知,競賽成績在在![]() 和
和![]() 分的人數,設受獎勵分數線為
分的人數,設受獎勵分數線為![]() ,列出方程即可求解;
,列出方程即可求解;
(Ⅱ)由(Ⅰ)知,利用分層抽樣,可知分數在![]() 的抽取2人,分數在
的抽取2人,分數在![]() 的抽取3人,設分數在
的抽取3人,設分數在![]() 的2人分別為
的2人分別為![]() ,分數在
,分數在![]() 的3人分別為
的3人分別為![]() ,利用古典概型及其概率的計算公式,即可求解.
,利用古典概型及其概率的計算公式,即可求解.
詳解:(Ⅰ)由頻率分布直方圖知,競賽成績在![]() 分的人數為
分的人數為![]() ,
,
競賽成績在![]() 的人數為
的人數為![]() ,
,
故受獎勵分數線在![]() 之間,
之間,
設受獎勵分數線為![]() ,則
,則![]() ,
,
解得![]() ,故受獎勵分數線為
,故受獎勵分數線為![]() .
.
(Ⅱ)由(Ⅰ)知,受獎勵的20人中,分數在![]() 的人數為8,分數在
的人數為8,分數在![]() 的人數為12,
的人數為12,
利用分層抽樣,可知分數在![]() 的抽取2人,分數在
的抽取2人,分數在![]() 的抽取3人,
的抽取3人,
設分數在![]() 的2人分別為
的2人分別為![]() ,分數在
,分數在![]() 的3人分別為
的3人分別為![]() ,
,
所有的可能情況有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,滿足條件的情況有
,滿足條件的情況有![]() ,
,![]() ,
,![]() ,所求的概率為
,所求的概率為![]() .
.


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:
【題目】某校有![]() ,
,![]() ,
,![]() ,
,![]() 四件作品參加航模類作品比賽.已知這四件作品中恰有兩件獲獎.在結果揭曉前,甲、乙、丙、丁四位同學對這四件參賽作品的獲獎情況預測如下:
四件作品參加航模類作品比賽.已知這四件作品中恰有兩件獲獎.在結果揭曉前,甲、乙、丙、丁四位同學對這四件參賽作品的獲獎情況預測如下:
甲說:“![]() 、
、![]() 同時獲獎”;
同時獲獎”;
乙說:“![]() 、
、![]() 不可能同時獲獎”;
不可能同時獲獎”;
丙說:“![]() 獲獎”;
獲獎”;
丁說:“![]() 、
、![]() 至少一件獲獎”.
至少一件獲獎”.
如果以上四位同學中有且只有二位同學的預測是正確的,則獲獎的作品是( )
A. 作品![]() 與作品
與作品![]() B. 作品
B. 作品![]() 與作品
與作品![]() C. 作品
C. 作品![]() 與作品
與作品![]() D. 作品
D. 作品![]() 與作品
與作品![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,直線l:
,直線l:![]() ,設圓C的半徑為1,圓心在l上.
,設圓C的半徑為1,圓心在l上.
![]() 若圓心C也在直線
若圓心C也在直線![]() 上,過A作圓C的切線,求切線方程;
上,過A作圓C的切線,求切線方程;
![]() 若圓C上存在點M,使
若圓C上存在點M,使![]() ,求圓心C的橫坐標a取值范圍.
,求圓心C的橫坐標a取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某產品的廣告費用x與銷售額y的統計數據如表:
廣告費用x(萬元) | 1 | 2 | 4 | 5 |
銷售額y(萬元) | 6 | 14 | 28 | 32 |
根據上表中的數據可以求得線性回歸方程 ![]() =
= ![]() x+
x+ ![]() 中的
中的 ![]() 為6.6,據此模型預報廣告費用為10萬元時銷售額為( )
為6.6,據此模型預報廣告費用為10萬元時銷售額為( )
A.66.2萬元
B.66.4萬元
C.66.8萬元
D.67.6萬元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為研究某藥品的療效,選取若干名志愿者進行臨床試驗,所有志愿者的舒張壓數據(單位:![]() )的分組區間為
)的分組區間為![]() ,
,![]() ,
,![]() ,
,![]() ,
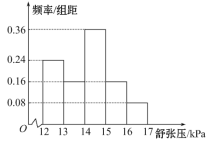
,![]() ,將其按從左到右的順序分別編號為第一組,第二組,......,第五組.如圖是根據試驗數據制成的頻率分布直方圖.已知第一組與第二組共有
,將其按從左到右的順序分別編號為第一組,第二組,......,第五組.如圖是根據試驗數據制成的頻率分布直方圖.已知第一組與第二組共有![]() 人,第三組中沒有療效的有
人,第三組中沒有療效的有![]() 人,則第三組中有療效的人數為( )
人,則第三組中有療效的人數為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
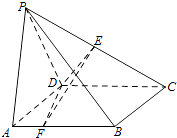
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是正方形,AD=PD=2,PA=2 ![]() ,∠PDC=120°,點E為線段PC的中點,點F在線段AB上. (Ⅰ)若AF=
,∠PDC=120°,點E為線段PC的中點,點F在線段AB上. (Ⅰ)若AF= ![]() ,求證:CD⊥EF;
,求證:CD⊥EF;
(Ⅱ)設平面DEF與平面DPA所成二面角的平面角為θ,試確定點F的位置,使得cosθ= ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】觀察下列等式:12=1,12﹣22=﹣3,12﹣22+32=6,12﹣22+32﹣42=﹣10,…由以上等式推測到一個一般的結論:對于n∈N* , 12﹣22+32﹣42+…+(﹣1)n+1n2= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com