Question

6．已知在長方體ABCD-A₁B₁C₁D₁中，E、M、N分別是BC、AE、D₁C的中點，AD=AA₁，AB=2AD
（Ⅰ）證明：MN∥平面ADD₁A₁
（Ⅱ）求直線AD與平面DMN所成角的余弦值．

Answer 1

分析 （1）如圖，建立空間直角坐標系，設AD=1，則AB=2．由DC⊥平面ADD₁A₁，可得$\overrightarrow{DC}$是平面ADD₁A₁的一個法向量．證明$\overrightarrow{MN}•\overrightarrow{DC}$=0，即可證明$MN∥平面AD{D_1}{A_1}\end{array}$．
（2）設平面DMN的一個法向量為$\overrightarrow{n}$=（x，y，z）．利用$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DM}=0}\\{\overrightarrow{n}•\overrightarrow{DN}=0}\end{array}\right.$，可得$\overrightarrow{n}$．利用sinθ=$\frac{|\overrightarrow{DA}•\overrightarrow{n}|}{|\overrightarrow{DA}||\overrightarrow{n}|}$即可得出．

解答 解：（1）如圖，建立空間直角坐標系，設AD=1，則AB=2．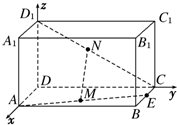
∵DC⊥平面ADD₁A₁，∴$\overrightarrow{DC}$=（0，2，0），就是平面ADD₁A₁的一個法向量．
$\begin{array}{l}∵M（\frac{3}{4}，1，0），N（0，1，\frac{1}{2}）$，∴$\overrightarrow{MN}=（-\frac{3}{4}，0，\frac{1}{2}）\\ 又∵\overrightarrow{MN}•\overrightarrow{DC}=0$，∴$\overrightarrow{MN}•\overrightarrow{DC}$=0，
∴$\overrightarrow{MN}⊥\overrightarrow{DC}\\∵MN?平面AD{D_1}{A_1}$，∴$MN∥平面AD{D_1}{A_1}\end{array}$．
（2）設平面DMN的一個法向量為$\overrightarrow n=（x，y，z），\overrightarrow{DA}=（1，0，0）$$\overrightarrow{DM}=（\frac{3}{4}，1，0），\overrightarrow{DN}=（0，1，\frac{1}{2}）$．
∴$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DM}=0}\\{\overrightarrow{n}•\overrightarrow{DN}=0}\end{array}\right.$，∴$\left\{\begin{array}{l}{\frac{3}{4}x+y=0}\\{y+\frac{1}{2}z=0}\end{array}\right.$．
取$\overrightarrow{n}$=$（\frac{4}{3}，-1，2）$．
∴sinθ=$\frac{|\overrightarrow{DA}•\overrightarrow{n}|}{|\overrightarrow{DA}||\overrightarrow{n}|}$=$\frac{4\sqrt{61}}{61}$．
所以直線DA與平面ADD₁A₁，所成角的正弦位值是$\frac{4\sqrt{61}}{61}$．

點評 本題考查了空間位置關系、法向量的意義、數量積運算性質、向量夾角公式，考查了推理能力與計算能力，屬于中檔題．