
【題目】已知橢圓![]() 的一個頂點為
的一個頂點為![]() ,右焦點為
,右焦點為![]() ,且
,且![]() ,其中
,其中![]() 為原點.
為原點.
(Ⅰ)求橢圓的方程;
(Ⅱ)已知點![]() 滿足
滿足![]() ,點
,點![]() 在橢圓上(
在橢圓上(![]() 異于橢圓的頂點),直線
異于橢圓的頂點),直線![]() 與以
與以![]() 為圓心的圓相切于點
為圓心的圓相切于點![]() ,且
,且![]() 為線段
為線段![]() 的中點.求直線
的中點.求直線![]() 的方程.
的方程.
科目:高中數學 來源: 題型:
【題目】設數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() .
.
(1)求證:數列![]() 為等比數列;
為等比數列;
(2)設數列![]() 的前
的前![]() 項和為
項和為![]() ,求證:
,求證: ![]() 為定值;
為定值;
(3)判斷數列![]() 中是否存在三項成等差數列,并證明你的結論.
中是否存在三項成等差數列,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在3世紀中期,我國古代數學家劉徽在《九章算術注》中提出了割圓術:“割之彌細,所失彌少,割之又割,以至于不可割,則與圓合體,而無所失矣”.這可視為中國古代極限觀念的佳作.割圓術可以視為將一個圓內接正![]() 邊形等分成
邊形等分成![]() 個等腰三角形(如圖所示),當
個等腰三角形(如圖所示),當![]() 變得很大時,等腰三角形的面積之和近似等于圓的面積.運用割圓術的思想,可得到sin3°的近似值為( )(
變得很大時,等腰三角形的面積之和近似等于圓的面積.運用割圓術的思想,可得到sin3°的近似值為( )(![]() 取近似值3.14)
取近似值3.14)
A.0.012B.0.052
C.0.125D.0.235
查看答案和解析>>
科目:高中數學 來源: 題型:
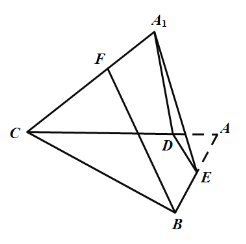
【題目】如圖,在邊長為4的正三角形![]() 中,E為邊
中,E為邊![]() 的中點,過E作
的中點,過E作![]() 于D.把
于D.把![]() 沿
沿![]() 翻折至
翻折至![]() 的位置,連結
的位置,連結![]() .翻折過程中,其中正確的結論是( )
.翻折過程中,其中正確的結論是( )
A.![]() ;
;
B.存在某個位置,使![]() ;
;
C.若![]() ,則
,則![]() 的長是定值;
的長是定值;
D.若![]() ,則四面體
,則四面體![]() 的體積最大值為
的體積最大值為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空氣質量指數PM2.5(單位:![]() )表示每立方米空氣中可入肺顆粒物的含量,這個值越高,就代表空氣污染越嚴重:
)表示每立方米空氣中可入肺顆粒物的含量,這個值越高,就代表空氣污染越嚴重:
PM2.5 日均濃度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 |
|
空氣質量級別 | 一級 | 二級 | 三級 | 四級 | 五級 | 六級 |
空氣質量類型 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
甲乙兩城市2020年5月份中的15天對空氣質量指數PM2.5進行監測,獲得PM2.5日均濃度指數數據如莖葉圖所示:
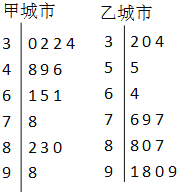
(1)根據你所學的統計知識估計甲乙兩城市15天內哪個城市空氣質量總體較好?并簡要說明理由.
(2)在15天內任取1天,估計甲乙兩城市空氣質量類別均為優或良的概率;
(3)在乙城市15個監測數據中任取2個,設![]() 為空氣質量類別為優或良的天數,求
為空氣質量類別為優或良的天數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() (
(![]() ,
,![]() )的部分圖象如圖所示,則下列結論正確的是( )
)的部分圖象如圖所示,則下列結論正確的是( )
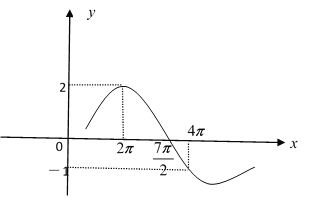
A.![]()
B.若把函數![]() 的圖像向左平移
的圖像向左平移![]() 個單位,則所得函數是奇函數
個單位,則所得函數是奇函數
C.若把![]() 的橫坐標縮短為原來的
的橫坐標縮短為原來的![]() 倍,縱坐標不變,得到的函數在
倍,縱坐標不變,得到的函數在![]() 上是增函數
上是增函數
D.![]() ,若
,若![]() 恒成立,則
恒成立,則![]() 的最小值為
的最小值為![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com