Question

2．函數f（x）=lnx在點P（x₀，f（x₀））處的切線l與函數lg（x）=e^x的圖象也相切，則滿足條件的切點P的個數有（　　）

• A． 0個
• B． 1個
• C． 2個
• D． 3個

Answer 1

分析 先求直線l為函數的圖象上一點A（x₀，f （x₀））處的切線方程，再設直線l與曲線y=g（x）相切于點（x₁，e${\;}^{{x}_{1}}$），進而可得lnx₀=$\frac{{x}_{0}+1}{{x}_{0}-1}$，即可得出結論．

解答 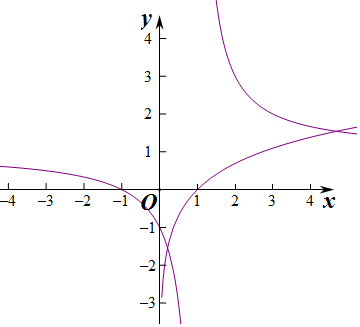解：∵f（x）=lnx，
∴f′（x）=$\frac{1}{x}$，
∴x=x₀，f′（x₀）=$\frac{1}{{x}_{0}}$，
∴切線l的方程為y-lnx₀=$\frac{1}{{x}_{0}}$（x-x₀），
即y=$\frac{1}{{x}_{0}}$x+lnx₀-1，①
設直線l與曲線y=g（x）
相切于點（x₁，e${\;}^{{x}_{1}}$），
∵g'（x）=e^x，∴e${\;}^{{x}_{1}}$=$\frac{1}{{x}_{0}}$，
∴x₁=-lnx₀．
∴直線l也為y-$\frac{1}{{x}_{0}}$=$\frac{1}{{x}_{0}}$（x+lnx₀），
即y=$\frac{1}{{x}_{0}}$x+$\frac{ln{x}_{0}}{{x}_{0}}$+$\frac{1}{{x}_{0}}$，②
由①②得lnx₀=$\frac{{x}_{0}+1}{{x}_{0}-1}$，
作出y=lnx和y=$\frac{x+1}{x-1}$的圖象，
如圖所示，圖象有兩個交點，方程有兩解．
故選：C．

點評 本題以函數為載體，考查導數知識的運用，考查曲線的切線，同時考查零點存在性定理，綜合性比較強．