
 若某市6所中學參加中學生合唱比賽的得分用莖葉圖表示如圖,其中莖為十位數,葉為個位數,則這組數據的方差是$\frac{13}{3}$.
若某市6所中學參加中學生合唱比賽的得分用莖葉圖表示如圖,其中莖為十位數,葉為個位數,則這組數據的方差是$\frac{13}{3}$. 分析 根據題意,由莖葉圖分析出所給的數據,根據數據先計算出數據的平均數,進而由方差公式計算可得答案.
解答 解:根據題意,由莖葉圖可得所給的數據為:87、91、93、92、90、93,
其平均數$\overline{x}$=$\frac{87+91+93+92+90+93}{6}$=91,
則其方差s2=$\frac{(87-91)^{2}+(91-91)^{2}+(93-91)^{2}+(92-9{1)}^{2}+({90-91)}^{2}+(93-91)^{2}}{6}$=$\frac{13}{3}$,
故答案為:$\frac{13}{3}$.
點評 本題考查莖葉圖的應用,涉及數據方差的計算,關鍵是由莖葉圖讀出數據.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ab2=9 | B. | a2b=9,a<0 | C. | b=9a2,a<0 | D. | b2=9a |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2,-2 | B. | -2,-2 | C. | $\frac{1}{2}$,2 | D. | $\frac{1}{2}$,$\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)>0恒成立 | B. | f(x)<0恒成立 | ||
| C. | f(x)的最大值為0 | D. | f(x)與0的大小關系不確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
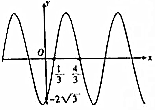
| A. | 函數f(x)的最小正周期為π | |
| B. | 函數f(x)的值域為[-$\frac{7}{2}$,$\frac{7}{2}$] | |
| C. | 函數f(x)的圖象關于直線x=-$\frac{1}{6}$對稱 | |
| D. | 函數f(x)的圖象向右平移$\frac{1}{3}$個單位得到函數y=Asinωx的圖象 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com