【題目】已知
的三個頂點落在半徑為
的球
的表面上，三角形有一個角為
且其對邊長為3，球心到所在的平面的距離恰好等于半徑的一半，點
為球面上任意一點，則
三棱錐的體積的最大值為（ ）
A. 
B. 
C. 
D. 
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，以坐標原點
為極點，
軸非負半軸為極軸且取相同的單位長度建立極坐標系.已知點
軌跡的參數方程為
（
，
為參數），點
在曲線
上.
（1）求點軌跡的普通方程和曲線
的直角坐標方程；
（2）求
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
的三個頂點落在半徑為
的球
的表面上，三角形有一個角為
且其對邊長為3，球心到所在的平面的距離恰好等于半徑的一半，點
為球面上任意一點，則
三棱錐的體積的最大值為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于函數
，若
，則稱
為的“不動點”，若
，則稱為的“穩定點”，函數的“不動點”和“穩定點”的集合分別記為
和
，即
，
，那么，
（1）求函數
的“穩定點”；
（2）求證：
；
（3）若
，且
，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設單調函數
的定義域為
，值域為
，如果單調函數
使得函數
的值域也是，則稱函數是函數的一個“保值域函數”．已知定義域為
的函數
，函數
與
互為反函數，且
是的一個“保值域函數”，是的一個“保值域函數”，則
__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直三棱柱ABC-A1B1C1中，D，E分別為AB，BC的中點，點F在側棱B1B上，且
， 
.
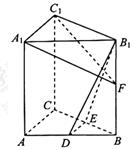
求證：（1）直線DE
平面A1C1F；
（2）平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設命題p：實數
滿足不等式
；
命題q：關于
不等式
對任意的
恒成立．
（1）若命題
為真命題，求實數的取值范圍；
（2）若“
”為假命題，“
”為真命題，求實數的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
