
(本題滿分16分)甲方是一農場,乙方是一工廠,由于乙方生產須占用甲方的資源,因此甲方每年向乙方索賠以彌補經濟損失并獲得一定凈收入.乙方在不賠付甲方的情況下,乙方的年利潤 (元)與年產量
(元)與年產量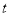 (噸)滿足函數關系
(噸)滿足函數關系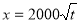 .若乙方每生產一噸產品必須賠付甲方
.若乙方每生產一噸產品必須賠付甲方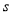 元(以下稱
元(以下稱 為賠付價格).
為賠付價格).
(Ⅰ)將乙方的年利潤w (元)表示為年產量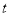 (噸)的函數,并求出乙方獲得最大利潤的年產量;
(噸)的函數,并求出乙方獲得最大利潤的年產量;
(Ⅱ)甲方每年受乙方生產影響的經濟損失金額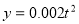 (元),在乙方按照獲得最大利潤的產量進行生產的前提下,甲方要在索賠中獲得最大凈收入,應向乙方要求的賠付價格
(元),在乙方按照獲得最大利潤的產量進行生產的前提下,甲方要在索賠中獲得最大凈收入,應向乙方要求的賠付價格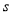 是多少?
是多少?
(Ⅰ) ,
,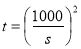 (Ⅱ)
(Ⅱ)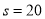
【解析】
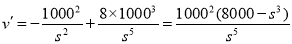 試題分析:(Ⅰ)解決利潤問題,關鍵分清年利潤與單位利潤,收益與支出:乙方的實際年利潤為乙方的年利潤減去每年賠付甲方額:
試題分析:(Ⅰ)解決利潤問題,關鍵分清年利潤與單位利潤,收益與支出:乙方的實際年利潤為乙方的年利潤減去每年賠付甲方額: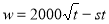
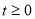 .這是關于
.這是關于 的二次函數,求其最值,須明確定義區間及對稱軸之間關系:當
的二次函數,求其最值,須明確定義區間及對稱軸之間關系:當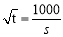 ,
,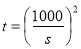 時,
時, 取得最大值;(Ⅱ)甲方凈收入為乙方每年賠付甲方額減去每年受乙方生產影響的經濟損失金額:甲方凈收入為
取得最大值;(Ⅱ)甲方凈收入為乙方每年賠付甲方額減去每年受乙方生產影響的經濟損失金額:甲方凈收入為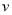 元,則
元,則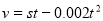 .
.
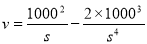 ,這需利用導數求其最值:
,這需利用導數求其最值:
令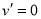 ,得
,得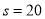 .當
.當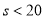 時,
時,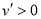 ;當
;當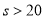 時,
時,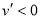 ,所以
,所以 時,
時,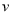 取得最大值.
取得最大值.
試題解析(Ⅰ)乙方的實際年利潤為: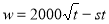
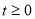 . (5分)
. (5分)
 ,
,
當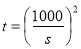 時,
時, 取得最大值.
取得最大值.
所以乙方取得最大年利潤的年產量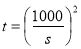 (噸).
(噸).
(Ⅱ)設甲方凈收入為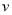 元,則
元,則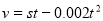 .
.
將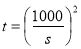 代入上式,得:
代入上式,得: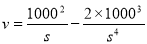 . (5分)
. (5分)
又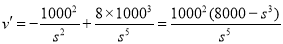
令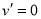 ,得
,得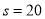 .
.
當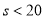 時,
時,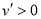 ;當
;當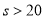 時,
時,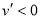 ,所以
,所以 時,
時,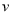 取得最大值.
取得最大值.
因此甲方向乙方要求賠付價格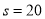 (元/噸)時,獲最大凈收入. (8分)
(元/噸)時,獲最大凈收入. (8分)
考點:利用導數求函數最值


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:2014-2015學年浙江省嘉興市高三新高考單科綜合調研三理科數學試卷(解析版) 題型:填空題
設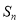 為數列
為數列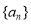 的前
的前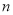 項和,若
項和,若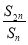
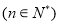 是非零常數,則稱該數列為“和等比數列”;若數列
是非零常數,則稱該數列為“和等比數列”;若數列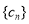 是首項為
是首項為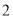 ,公差為
,公差為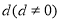 的等差數列,且數列
的等差數列,且數列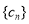 是“和等比數列”,則
是“和等比數列”,則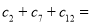 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com