
【題目】如圖,扇形AOB是一個觀光區的平面示意圖,其中圓心角∠AOB為![]() ,半徑OA為1 km.為了便于游客觀光休閑,擬在觀光區內鋪設一條從入口A到出口B的觀光道路,道路由弧AC、線段CD及線段DB組成,其中D在線段OB上,且CD∥AO.設∠AOC=θ.
,半徑OA為1 km.為了便于游客觀光休閑,擬在觀光區內鋪設一條從入口A到出口B的觀光道路,道路由弧AC、線段CD及線段DB組成,其中D在線段OB上,且CD∥AO.設∠AOC=θ.
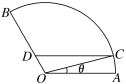
(1)用θ表示CD的長度,并寫出θ的取值范圍;
(2)當θ為何值時,觀光道路最長?
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用![]() 表示CD的長度的關鍵是在
表示CD的長度的關鍵是在![]() 中正確利用正弦定理;
中正確利用正弦定理;
(2)首先將道路長度![]() 表達成
表達成![]() 的函數關系式,再利用導數方法研究函數的最大值,從而可以求得
的函數關系式,再利用導數方法研究函數的最大值,從而可以求得![]() 時,觀光道路最長.
時,觀光道路最長.
(1)在△OCD中,由正弦定理,得
![]() =
=![]() =
=![]() =
=![]() ,
,
所以CD=![]() sin
sin![]() =cos θ+
=cos θ+![]() sin θ,OD=
sin θ,OD=![]() sin θ,
sin θ,
因為OD<OB,即![]() sin θ<1,所以sin θ<
sin θ<1,所以sin θ<![]() ,所以0<θ<
,所以0<θ<![]() ,
,
所以CD=cos θ+![]() sin θ,θ的取值范圍為
sin θ,θ的取值范圍為![]() .
.
(2)設觀光道路長度為L(θ),
則L(θ)=BD+CD+弧CA的長
=1-![]() sin θ+cos θ+
sin θ+cos θ+![]() sin θ+θ
sin θ+θ
=cos θ-![]() sin θ+θ+1,θ∈
sin θ+θ+1,θ∈![]() ,
,
L′(θ)=-sin θ-![]() cos θ+1,
cos θ+1,
由L′(θ)=0,得sin![]() =
=![]() ,
,
又θ∈![]() ,所以θ=
,所以θ=![]() ,
,
列表:
θ |
|
|
|
L′(θ) | + | 0 | - |
L(θ) | 增函數 | 極大值 | 減函數 |
所以當θ=![]() 時,L(θ)達到最大值,即當θ=
時,L(θ)達到最大值,即當θ=![]() 時,觀光道路最長.
時,觀光道路最長.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:高中數學 來源: 題型:
【題目】某城市為了解游客人數的變化規律,提高旅游服務質量,收集并整理了2017年1月至2019年12月期間月接待游客量(單位:萬人)的數據,繪制了下面的折線圖.根據該折線圖,下列結論錯誤的是( )
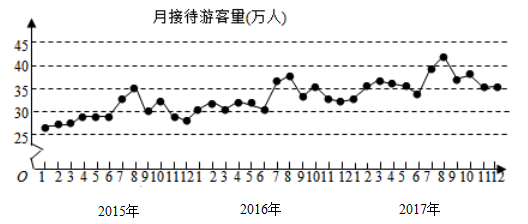
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位數為30萬人
D.各年1月至6月的月接待游客量相對于7月至12月,波動性更小,變化比較平穩
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1.

(1)求證:AB1⊥平面A1BC1;
(2)若D在B1C1上,滿足B1D=2DC1,求AD與平面A1BC1所成的角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,若橢圓經過點
,若橢圓經過點![]() ,且△PF1F2的面積為2.
,且△PF1F2的面積為2.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設斜率為1的直線![]() 與以原點為圓心,半徑為
與以原點為圓心,半徑為![]() 的圓交于A,B兩點,與橢圓C交于C,D兩點,且
的圓交于A,B兩點,與橢圓C交于C,D兩點,且![]() (
(![]() ),當
),當![]() 取得最小值時,求直線
取得最小值時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圓錐![]() (其中
(其中![]() 為頂點,
為頂點,![]() 為底面圓心)的側面積與底面積的比是
為底面圓心)的側面積與底面積的比是![]() ,則圓錐
,則圓錐![]() 與它外接球(即頂點在球面上且底面圓周也在球面上)的體積比為( )
與它外接球(即頂點在球面上且底面圓周也在球面上)的體積比為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查國企員工對新個稅法的滿意程度,研究人員在![]() 地各個國企中隨機抽取了1000名員工進行調查,并將滿意程度以分數的形式統計成如下的頻率分布表,其中
地各個國企中隨機抽取了1000名員工進行調查,并將滿意程度以分數的形式統計成如下的頻率分布表,其中![]() .(計算結果保留兩位小數)
.(計算結果保留兩位小數)
分數 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
頻率 | 0.08 |
| 0.35 | 0.27 |
|
(1)試估計被調查的員工的滿意程度的中位數;
(2)若把每組的組中值作為該組的滿意程度,試估計被調查的員工的滿意程度的平均數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() ,其中
,其中![]() ,函數
,函數![]() 與
與![]() 關于直線
關于直線![]() 對稱.
對稱.
(1)若函數![]() 在區間
在區間![]() 上遞增,求a的取值范圍;
上遞增,求a的取值范圍;
(2)證明:![]() ;
;
(3)設![]() ,其中
,其中![]() 恒成立,求滿足條件的最小正整數b的值.
恒成立,求滿足條件的最小正整數b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】點![]() 與定點
與定點![]() 的距離和它到直線
的距離和它到直線![]() 的距離的比是常數
的距離的比是常數![]() ,設點
,設點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,設
兩點,設![]() 的中點為
的中點為![]() ,
,![]() ,
,![]() 兩點為曲線
兩點為曲線![]() 上關于原點
上關于原點![]() 對稱的兩點,且
對稱的兩點,且![]() (
(![]() ),求四邊形
),求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com