
【題目】在平面直角坐標系![]() 中,己知圓
中,己知圓![]() ,且圓
,且圓![]() 被直線
被直線![]() 截得的弦長為2.
截得的弦長為2.
(1)求圓![]() 的標準方程;
的標準方程;
(2)若圓![]() 的切線
的切線![]() 在
在![]() 軸和
軸和![]() 軸上的截距相等,求切線
軸上的截距相等,求切線![]() 的方程;
的方程;
(3)若圓![]() 上存在點
上存在點![]() ,由點
,由點![]() 向圓
向圓![]() 引一條切線,切點為
引一條切線,切點為![]() ,且滿足
,且滿足![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)將圓方程整理為標準方程形式,可知![]() ,得到圓心坐標和半徑;由垂徑定理可利用弦長構造出關于
,得到圓心坐標和半徑;由垂徑定理可利用弦長構造出關于![]() 的方程,解方程求得
的方程,解方程求得![]() ,從而得到標準方程;(2)分為直線
,從而得到標準方程;(2)分為直線![]() 過原點和不過原點兩種情況,分別假設直線方程,利用圓心到直線距離等于半徑可構造方程求得結果;(3)設
過原點和不過原點兩種情況,分別假設直線方程,利用圓心到直線距離等于半徑可構造方程求得結果;(3)設![]() ,根據
,根據![]() 且
且![]() 可整理出
可整理出![]() 點軌跡方程為:
點軌跡方程為:![]() ;根據
;根據![]() 在圓
在圓![]() 上,則兩圓有公共點,根據圓與圓位置關系的判定可構造不等式,解不等式求得結果.
上,則兩圓有公共點,根據圓與圓位置關系的判定可構造不等式,解不等式求得結果.
(1)圓![]() 方程可整理為:
方程可整理為:![]()
![]()
![]() 圓
圓![]() 的圓心坐標為
的圓心坐標為![]() ,半徑
,半徑![]()
![]() 圓心
圓心![]() 到直線
到直線![]() 的距離:
的距離: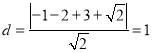
![]() 截得的弦長為:
截得的弦長為:![]() ,解得:
,解得:![]()
![]() 圓
圓![]() 的標準方程為:
的標準方程為:![]()
(2)①若直線![]() 過原點,可假設直線
過原點,可假設直線![]() 方程為:
方程為:![]() ,即
,即![]()
![]() 直線
直線![]() 與圓相切
與圓相切 ![]() 圓心到直線距離
圓心到直線距離![]() ,解得:
,解得:![]()
![]() 切線
切線![]() 方程為:
方程為:![]()
②若直線![]() 不過原點,可假設直線
不過原點,可假設直線![]() 方程為:
方程為:![]() ,即
,即![]()
![]() 圓心到直線距離
圓心到直線距離![]() ,解得:
,解得:![]() 或
或![]()
![]() 切線
切線![]() 方程為
方程為![]() 或
或![]()
綜上所述,切線![]() 方程為
方程為![]() 或
或![]() 或
或![]()
(3)假設![]()
![]() ,即
,即![]()
又直線![]() 與圓
與圓![]() 相切,切點為
相切,切點為![]()
![]()
即:![]() ,整理得:
,整理得:![]()
![]() 又在圓
又在圓![]() 上
上 ![]() 兩圓有公共點
兩圓有公共點
![]() ,解得:
,解得:![]()
即![]() 的取值范圍為:
的取值范圍為:![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】貨車欲以xkm/h的速度行駛,去130km遠的某地,按交通法規,限制x的允許范圍是50≤x≤100,假設汽油的價格為2元/升,而汽車耗油的速率是![]() 升/小時.司機的工資是14元/小時,試問最經濟的車速是多少?這次行車往返的總費用最低是多少?
升/小時.司機的工資是14元/小時,試問最經濟的車速是多少?這次行車往返的總費用最低是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A. “f(0)![]() ”是“函數f(x)是奇函數”的充要條件
”是“函數f(x)是奇函數”的充要條件
B. 若p:![]() ,
,![]() ,則
,則![]() :
:![]() ,
,![]()
C. “若![]() ,則
,則![]() ”的否命題是“若
”的否命題是“若![]() ,則
,則![]() ”
”
D. 若![]() 為假命題,則p,q均為假命題
為假命題,則p,q均為假命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班級有3名同學報名參加學校組織的辯論賽,現有甲、乙兩個辨題可以選擇,學校決定讓選手以抽取卡片(除上面標的數不同外其他完全相同)的方式選擇辯題,且每名選手抽取后放回.已知共有10張卡片,卡片上分別標有![]() 共10個數.若抽到卡片上的數為質數(2,3,5,7),則選擇甲辨題,否則選擇乙辯題.
共10個數.若抽到卡片上的數為質數(2,3,5,7),則選擇甲辨題,否則選擇乙辯題.
(1)求這3名同學中至少有1人選擇甲辨題的概率.
(2)用X、Y分別表示這3名同學中選擇甲、乙辨題的人數,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】撫州市某中學利用周末組織教職員工進行了一次秋季登軍峰山健身的活動,有![]() 人參加,現將所有參加人員按年齡情況分為
人參加,現將所有參加人員按年齡情況分為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 等七組,其頻率分布直方圖如下圖所示.已知
等七組,其頻率分布直方圖如下圖所示.已知![]() 之間的參加者有4人.
之間的參加者有4人.
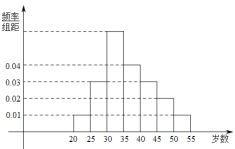
(1)求![]() 和
和![]() 之間的參加者人數
之間的參加者人數![]() ;
;
(2)組織者從![]() 之間的參加者(其中共有
之間的參加者(其中共有![]() 名女教師包括甲女,其余全為男教師)中隨機選取
名女教師包括甲女,其余全為男教師)中隨機選取![]() 名擔任后勤保障工作,求在甲女必須入選的條件下,選出的女教師的人數為2人的概率.
名擔任后勤保障工作,求在甲女必須入選的條件下,選出的女教師的人數為2人的概率.
(3)已知![]() 和
和![]() 之間各有
之間各有![]() 名數學教師,現從這兩個組中各選取
名數學教師,現從這兩個組中各選取![]() 人擔任接待工作,設兩組的選擇互不影響,求兩組選出的人中都至少有
人擔任接待工作,設兩組的選擇互不影響,求兩組選出的人中都至少有![]() 名數學教師的概率?
名數學教師的概率?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的三個頂點分別為A(﹣3,0),B(2,1),C(﹣2,3),試求:
(1)邊AC所在直線的方程;
(2)BC邊上的中線AD所在直線的方程;
(3)BC邊上的高AE所在直線的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】珠海市某學校的研究性學習小組,對晝夜溫差(最高溫度與最低溫度的差)大小與綠豆種子一天內出芽數之間的關系進行了研究,該小組在4月份記錄了1日至6日每天晝夜最高、最低溫度(如圖1),以及浸泡的![]() 顆綠豆種子當天內的出芽數(如圖2)
顆綠豆種子當天內的出芽數(如圖2)
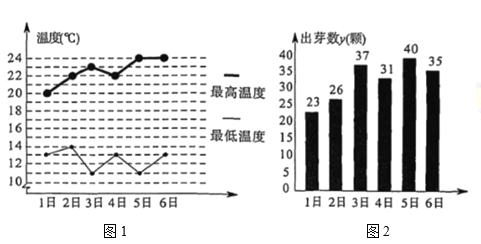
已知綠豆種子出芽數![]() (顆) 和溫差
(顆) 和溫差![]() 具有線性相關關系.
具有線性相關關系.
(1)求綠豆種子出芽數![]() (顆)關于溫差
(顆)關于溫差![]() 的回歸方程
的回歸方程![]() ;
;
(2)假如4月1日至7日的日溫差的平均值為![]() ,估計4月7日浸泡的
,估計4月7日浸泡的![]() 顆綠豆種子一天內的出芽數.
顆綠豆種子一天內的出芽數.
附: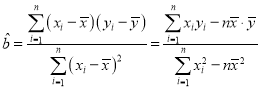 ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com