
【題目】已知![]() .
.
(1)當![]() 時,求不等式
時,求不等式![]() 的解集;
的解集;
(2)若![]() 時,不等式
時,不等式![]() 恒成立,求a的取值范圍.
恒成立,求a的取值范圍.
【答案】(1) ![]() .(2)
.(2) ![]() .
.
【解析】
(1)將a=1代入f(x)中,去絕對值后分別解不等式即可;
(2)x∈(0,1)時,不等式f(x)<x+2恒成立等價于當x∈(0,1)時,|ax-1|<1恒成立,然后分a≤0和a>0討論即可.
解:(1)解法1:當![]() 時,不等式
時,不等式![]() 可化簡為
可化簡為![]() .
.
當![]() 時,
時,![]() ,解得
,解得![]() ,所以
,所以![]() ;
;
當![]() 時,
時,![]() ,
,![]() ,無解;
,無解;
當![]() 時,
時,![]() ,解得
,解得![]() ,所以
,所以![]() ﹒
﹒
綜上,不等式![]() 的解集為
的解集為![]() .
.
解法2:當![]() 時,
時,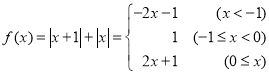
當![]() 時,
時,![]() ,解得
,解得![]() ,所以
,所以![]() ;
;
當![]() 時,
時,![]() ,無解;
,無解;
當![]() 時,
時,![]() ,解得
,解得![]() ,所以
,所以![]() .
.
綜上,不等式![]() 的解集為
的解集為![]() .
.
(2)解法1:當![]() 時,不等式
時,不等式![]() 可化簡為
可化簡為![]() .
.
令![]() ,則
,則![]() 的圖像為過定點
的圖像為過定點![]() 斜率為a的一條直線,
斜率為a的一條直線,
數形結合可知,當![]() 時,
時,![]() 在
在![]() 上恒成立.
上恒成立.
所以,所求a的取值范圍為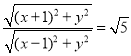
解法2:當![]() 時,不等式
時,不等式![]() 可化簡為
可化簡為![]() .
.
由不等式的性質得![]() 或
或![]() ,
,
即![]() 或
或![]() .
.
當![]() 時,
時,![]() ,不等式
,不等式![]() 不恒成立;
不恒成立;
為使不等式![]() 恒成立,則
恒成立,則![]() .
.
綜上,所求a的取值范圍為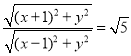 .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() +
+![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為![]() ,F為橢圓C的右焦點,A是右準線與x軸的交點,且AF=1.
,F為橢圓C的右焦點,A是右準線與x軸的交點,且AF=1.

(1)求橢圓C的方程;
(2)過橢圓C上頂點B的直線l交橢圓另一點D,交x軸于點M,若![]() ,求直線l的方程;
,求直線l的方程;
(3)設點![]() ,過點F且斜率不為零的直線m與橢圓C交于S,T兩點,直線TQ與直線x=2交于點S1,試問
,過點F且斜率不為零的直線m與橢圓C交于S,T兩點,直線TQ與直線x=2交于點S1,試問![]() 是否為定值?若是,求出這個定值,若不是,請說明理由.
是否為定值?若是,求出這個定值,若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于集合![]() ,
,![]() ,
,![]() ,
,![]() .集合
.集合![]() 中的元素個數記為
中的元素個數記為![]() .規定:若集合
.規定:若集合![]() 滿足
滿足![]() ,則稱集合
,則稱集合![]() 具有性質
具有性質![]() .
.
(I)已知集合![]() ,
,![]() ,寫出
,寫出![]() ,
,![]() 的值;
的值;
(II)已知集合![]() ,
,![]() 為等比數列,
為等比數列,![]() ,且公比為
,且公比為![]() ,證明:
,證明:![]() 具有性質
具有性質![]() ;
;
(III)已知![]() 均有性質
均有性質![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 年以來精準扶貧政策的落實,使我國扶貧工作有了新進展,貧困發生率由
年以來精準扶貧政策的落實,使我國扶貧工作有了新進展,貧困發生率由![]() 年底的
年底的![]() 下降到
下降到![]() 年底的
年底的![]() ,創造了人類減貧史上的的中國奇跡.“貧困發生率”是指低于貧困線的人口占全體人口的比例,
,創造了人類減貧史上的的中國奇跡.“貧困發生率”是指低于貧困線的人口占全體人口的比例,![]() 年至
年至![]() 年我國貧困發生率的數據如下表:
年我國貧困發生率的數據如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
貧困發生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)從表中所給的![]() 個貧困發生率數據中任選兩個,求兩個都低于
個貧困發生率數據中任選兩個,求兩個都低于![]() 的概率;
的概率;
(2)設年份代碼![]() ,利用線性回歸方程,分析
,利用線性回歸方程,分析![]() 年至
年至![]() 年貧困發生率
年貧困發生率![]() 與年份代碼
與年份代碼![]() 的相關情況,并預測
的相關情況,并預測![]() 年貧困發生率.
年貧困發生率.
附:回歸直線![]() 的斜率和截距的最小二乘估計公式分別為:
的斜率和截距的最小二乘估計公式分別為:
 (
(![]() 的值保留到小數點后三位)
的值保留到小數點后三位)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面ABCD是菱形,PA=PD,∠DAB=60°.
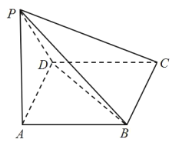
(1)證明:AD⊥PB.
(2)若PB=![]() ,AB=PA=2,求三棱錐P-BCD的體積。
,AB=PA=2,求三棱錐P-BCD的體積。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某人承攬一項業務,需做文字標牌4個,繪畫標牌5個,現有兩種規格的原料,甲種規格每張3m2,可做文字標牌1個,繪畫標牌2個,乙種規格每張2m2,可做文字標牌2個,繪畫標牌1個,求兩種規格的原料各用多少張,才能使總的用料面積最小?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,己知圓
中,己知圓![]() ,且圓
,且圓![]() 被直線
被直線![]() 截得的弦長為2.
截得的弦長為2.
(1)求圓![]() 的標準方程;
的標準方程;
(2)若圓![]() 的切線
的切線![]() 在
在![]() 軸和
軸和![]() 軸上的截距相等,求切線
軸上的截距相等,求切線![]() 的方程;
的方程;
(3)若圓![]() 上存在點
上存在點![]() ,由點
,由點![]() 向圓
向圓![]() 引一條切線,切點為
引一條切線,切點為![]() ,且滿足
,且滿足![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com