日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
設二次方程anx2-an+1x+1=0（n=1，2，3，…）有兩個根α和β且滿足6α-2αβ+6β=3.

（1）試用an來表示an+1；

（2）求證：{an-}是等比數列；

（3）當a1=時，求數列｛an｝的通項公式.

思路解析：這是一道有關數列、二次方程的根與系數關系的綜合題.根據題目條件給出的等量關系，找出遞推關系是解決問題的關鍵.

解：（1）由條件，據韋達定理知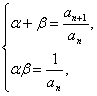

并代入已知條件6（α+β）-2αβ=3，

得=3.

∴an+1=an+.

兩邊同時減去，得an+1-=an-=(an-).

（2）由an+1=an+，

∴數列{an,-}是以為公比的等比數列.

（3）當a1=時，a1-=.

因此，數列{an,-}是以為首項，為公比的等比數列.

(an-)= ·()n-1.

∴an=+()n.

深化升華

本題中第（2）題的難點是如何發現在an+1=an+的兩邊同時減去.其方法是：設an+1+α=

（an+α），則an+1+α=an+α.

∴an+1=an-α，與an+1=an+對照，有-α=，

∴α=-.

一般地，對于形如an+1=can+d的遞推關系式，可以變形為（an+1-a）=c（an-a），使｛an-a｝成為一個等比數列，從而得到｛an｝的通項公式.

把條件中的遞推關系轉化到我們熟悉的等比數列中來研究，體現了數學中的化歸思想.


練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

設二次方程anx2-an+1x+1=0（n∈N*）有兩根α、β，且滿足6α-2αβ+6β=3．
（1）試用an表示an+1；
（2）求證：{an-
2
3
}是等比數列；
（3）若a1=
7
6
，求數列{an}的通項公式．

查看答案和解析>>

科目：高中數學 來源： 題型：

設二次方程anx2-an+1x+1=0(n∈N*)有兩個實根α和β，且滿足6α-2αβ+6β=3．
（1）試用an表示an+1；
（2）求證：{an-
23
}是等比數列．

查看答案和解析>>

科目：高中數學 來源： 題型：

設二次方程anx2-an+1x+1=0，n∈N+有兩根α和β，且滿足6α-2αβ+6β=3，a1=1
（1）試用an表示an+1；            
（2）證明{an-
2
3
}是等比數列；
（3）設cn=n•(an-
2
3
)，n∈N+，Tn為{cn}的前n項和，證明：Tn＜
4
3
（n∈N+）．

查看答案和解析>>

科目：高中數學 來源： 題型：

設二次方程anx2-an+1x+1=0，n∈N+有兩根α和β，且滿足6α-2αβ+6β=3，a1=1
（1）試用an表示an+1；
（2）證明{an-
2
3
}是等比數列；
（3）設cn=n•(an-
2
3
)，n∈N+，Tn為{cn}的前n項和，證明Tn＜2，（n∈N*）．

查看答案和解析>>

科目：高中數學 來源： 題型：

設二次方程anx2-an+1x+1=0，n∈N+有兩根α和β，且滿足6α-2αβ+6β=3，a1=1．
（1）證明：{an-
2
3
}是等比數列，并求{an}的通項公式；
（2）設cn=n•(an-
2
3
)，n∈N+，Tn為{cn}的前n項和，證明：Tn＜2，（n∈N+）．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 伊人影院在线观看 | 四虎影院最新网址 | 国产精品一区二区三区在线 | 亚洲国产高清视频 | 欧美日韩第一页 | 欧美日韩精品一区 | 成人国产免费视频 | 日本精品在线播放 | 日韩精品视频在线播放 | 国产成人涩涩涩视频在线观看 | www.日韩在线视频 | 四虎成人av | 久久人人爽人人爽 | 黄视频网站免费看 | 污网址在线看 | av在线免费观看一区二区 | 久久99国产精品久久99果冻传媒 | 亚洲天堂美女视频 | 夜久久 | 天天操夜夜操 | 国产日韩在线视频 | 亚洲国产情侣自拍 | 久久久久久久 | 日韩欧美视频 | 高清久久| 中文字幕av免费 | 亚洲国产91 | 国产成人av一区二区三区 | 亚洲精品在线看 | 亚洲第一页中文字幕 | 精品视频免费观看 | 国产乱码精品一品二品 | 亚洲精品电影 | 亚洲欧美一区二区精品中文字幕 | av片在线观看 | 日韩精品av一区二区三区 | 美女久久 | 亚洲人成电影网 | 蜜臀av国产精品久久久久 | 色综合天天综合网国产成人网 | 免费xxxxx在线观看网站软件 |