
| 單價x(萬元) | 8 | 8.2 | 8.4 | 8.8 | 8.6 | 9 |
| 銷量y(件) | 90 | 84 | 83 | 75 | 80 | 68 |
分析 (1)①根據公式求出$\widehat{b}$和$\widehat{a}$的值,求出回歸方程即可;②根據b的值判斷即可;(2)求出關于w的表達式,結合二次函數的性質求出w的最大值即可.
解答 解:(1)①依題意:$\stackrel{∧}{b}$=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$=-20,
$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=80+20×8.5=250,
∴回歸直線的方程為y=-20x+250;
②由于$\widehat{b}$=-20<0,則x,y負相關,
故隨定價的增加,銷量不斷降低.
(2)設科研所所得利潤為w,設定價為x,
∴w=(x-4.5)(-20x+250)=-20x2+340x-1125,
∴當$x=\frac{340}{40}=8.5$時,wmax=320,
故當定價為8.5元時,w取得最大值.
點評 本題考查了回歸方程問題,考查二次函數的性質,是一道基礎題.


科目:高中數學 來源: 題型:解答題
 已知F1、F2分別為橢圓C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上、下焦點,其中F1也是拋物線C2:x2=4y的焦點,點M是C1與C2在第二象限的交點,且|MF1|=$\frac{5}{3}$.
已知F1、F2分別為橢圓C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上、下焦點,其中F1也是拋物線C2:x2=4y的焦點,點M是C1與C2在第二象限的交點,且|MF1|=$\frac{5}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
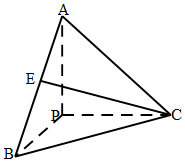 已知如圖,PA、PB、PC互相垂直,且長度相等,E為AB中點,則直線CE與平面PAC所成角的正弦值為$\frac{\sqrt{6}}{6}$.
已知如圖,PA、PB、PC互相垂直,且長度相等,E為AB中點,則直線CE與平面PAC所成角的正弦值為$\frac{\sqrt{6}}{6}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若a∥α,b∥α,則a∥b | B. | 若a∥α,b∥β,a∥b,則α∥β | ||
| C. | 若a⊥α,a?β,則α⊥β | D. | 若a,b在α內的射影相互垂直,則a⊥b |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {5,7} | B. | {1,3,9} | C. | {3,5,7} | D. | {1,2,3} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com