
【題目】在△ABC中,a,b,c分別是角A,B,C的對邊,且acosC=(2b﹣c)cosA.
(1)若![]() 3,求△ABC的面積;
3,求△ABC的面積;
(2)若∠B<∠C,求2cos2B+cos2C的取值范圍.
【答案】(1)![]() (2)(
(2)(![]() ,
,![]() ).
).
【解析】
(1)利用正弦定理可求角A,結合數量積![]() 3,可求△ABC的面積;
3,可求△ABC的面積;
(2)結合角之間的關系,把2cos2B+cos2C化簡為![]() ,然后結合角
,然后結合角![]() 的范圍可求.
的范圍可求.
(1)∵acosC=(2b﹣c)cosA,
∴由正弦定理可得sinAcosC=(2sinB﹣sinC)cosA,可得sinAcosC+sinCcosA=sin(A+C)=sinB=2sinBcosA,
∵B為三角形內角,sinB≠0,
∴cosA![]() ,
,
又∵A∈(0,π),
∴A![]() ,
,
∵![]() bccosA
bccosA![]() bc=3,可得bc=6,
bc=3,可得bc=6,
∴S△ABC![]() bcsinA
bcsinA![]() .
.
(2)∵∠B<∠C,C![]() B,可得B∈(0,
B,可得B∈(0,![]() ),
),
∴2B![]() ∈(
∈(![]() ,
,![]() ),
),
∴cos(2B![]() )∈(
)∈(![]() ,
,![]() ),
),
∴2cos2B+cos2C=1+cos2B![]() cos2B
cos2B![]() cos2(
cos2(![]() B)
B)![]() cos2B
cos2B![]() cos2B
cos2B![]() sin2B
sin2B![]() cos(2B
cos(2B![]() )∈(
)∈(![]() ,
,![]() ).
).
∴2cos2B+cos2C的取值范圍(![]() ,
,![]() ).
).


 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,已知點![]() ,
,![]() ,動點
,動點![]() 滿足直線
滿足直線![]() 與
與![]() 的斜率之積為
的斜率之積為![]() .記點
.記點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求![]() 的方程,并說明
的方程,并說明![]() 是什么曲線;
是什么曲線;
(2)若![]() ,
,![]() 是曲線
是曲線![]() 上的動點,且直線
上的動點,且直線![]() 過點
過點![]() ,問在
,問在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() ?若存在,請求出定點
?若存在,請求出定點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某無縫鋼管廠只生產甲、乙兩種不同規格的鋼管,鋼管有內外兩個口徑,甲種鋼管內外兩口徑的標準長度分別為![]() 和
和![]() ,乙種鋼管內外兩個口徑的標準長度分別為
,乙種鋼管內外兩個口徑的標準長度分別為![]() 和
和![]() .根據長期的生產結果表明,兩種規格鋼管每根的長度
.根據長期的生產結果表明,兩種規格鋼管每根的長度![]() 都服從正態分布
都服從正態分布![]() ,長度在
,長度在![]() 之外的鋼管為廢品,要回爐熔化,不準流入市場,其他長度的鋼管為正品.
之外的鋼管為廢品,要回爐熔化,不準流入市場,其他長度的鋼管為正品.
(1)在該鋼管廠生產的鋼管中隨機抽取10根進行檢測,求至少有1根為廢品的概率;
(2)監管部門規定每種規格鋼管的“口徑誤差”的計算方式為:若鋼管的內外兩個口徑實際長分別為![]() ,標準長分別為
,標準長分別為![]() ,則“口徑誤差”為
,則“口徑誤差”為![]() ,按行業生產標準,其中“一級品”“二級品”“合格品”的“口徑誤差”的范圍分別是
,按行業生產標準,其中“一級品”“二級品”“合格品”的“口徑誤差”的范圍分別是![]() (正品鋼管中沒有“口徑誤差”大于
(正品鋼管中沒有“口徑誤差”大于![]() 的鋼管),現分別從甲、乙兩種產品的正品中各隨機抽取100根,分別進行“口徑誤差”的檢測,統計后,繪制其頻率分布直方圖如圖所示:
的鋼管),現分別從甲、乙兩種產品的正品中各隨機抽取100根,分別進行“口徑誤差”的檢測,統計后,繪制其頻率分布直方圖如圖所示:
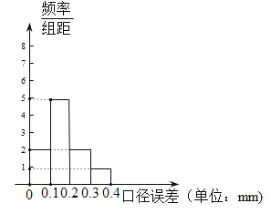

甲種鋼管 乙種鋼管
已知經銷商經銷甲種鋼管,其中“一級品”的利潤率為0.3,“二級品”的利潤率為0.18,“合格品”的利潤率為0.1;經銷乙種鋼管,其中“一級品”的利潤率為0.25,“二級品”的利潤率為0.15,“合格品”的利潤率為0.08,若視頻率為概率.
(ⅰ)若經銷商對甲、乙兩種鋼管各進了100萬元的貨,![]() 和
和![]() 分別表示經銷甲、乙兩種鋼管所獲得的利潤,求
分別表示經銷甲、乙兩種鋼管所獲得的利潤,求![]() 和
和![]() 的數學期望和方差,并由此分析經銷商經銷兩種鋼管的利弊;
的數學期望和方差,并由此分析經銷商經銷兩種鋼管的利弊;
(ⅱ)若經銷商計劃對甲、乙兩種鋼管總共進100萬元的貨,則分別在甲、乙兩種鋼管上進貨多少萬元時,可使得所獲利潤的方差和最小?
附:若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校要在一條水泥路邊安裝路燈,其中燈桿的設計如圖所示,AB為地面,CD,CE為路燈燈桿,CD⊥AB,∠DCE=![]() ,在E處安裝路燈,且路燈的照明張角∠MEN=
,在E處安裝路燈,且路燈的照明張角∠MEN=![]() .已知CD=4m,CE=2m.
.已知CD=4m,CE=2m.
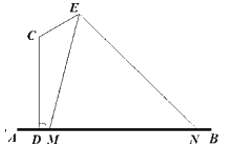
(1)當M,D重合時,求路燈在路面的照明寬度MN;
(2)求此路燈在路面上的照明寬度MN的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校健康社團為調查本校大學生每周運動的時長,隨機選取了80名學生,調查他們每周運動的總時長(單位:小時),按照![]()
![]()
![]()
![]()
![]()
![]() 共6組進行統計,得到男生、女生每周運動的時長的統計如下(表1、2),規定每周運動15小時以上(含15小時)的稱為“運動合格者”,其中每周運動25小時以上(含25小時)的稱為“運動達人”.
共6組進行統計,得到男生、女生每周運動的時長的統計如下(表1、2),規定每周運動15小時以上(含15小時)的稱為“運動合格者”,其中每周運動25小時以上(含25小時)的稱為“運動達人”.
表1:男生
時長 |
|
|
|
|
|
|
人數 | 2 | 8 | 16 | 8 | 4 | 2 |
表2:女生
時長 |
|
|
|
|
|
|
人數 | 0 | 4 | 12 | 12 | 8 | 4 |
(1)從每周運動時長不小于20小時的男生中隨機選取2人,求選到“運動達人”的概率;
(2)根據題目條件,完成下面![]() 列聯表,并判斷能否有99%的把握認為本校大學生是否為“運動合格者”與性別有關.
列聯表,并判斷能否有99%的把握認為本校大學生是否為“運動合格者”與性別有關.
每周運動的時長小于15小時 | 每周運動的時長不小于15小時 | 總計 | |
男生 | |||
女生 | |||
總計 | |||
參考公式: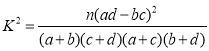 ,其中
,其中![]() .
.
參考數據:
| 0.40 | 0.25 | 0.10 | 0.010 |
| 0.708 | 1.323 | 2.706 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,底面
,底面![]() 為正方形,且
為正方形,且![]() .若四棱錐
.若四棱錐![]() 的每個頂點都在球
的每個頂點都在球![]() 的球面上,則球
的球面上,則球![]() 的表面積的最小值為_____;當四棱錐
的表面積的最小值為_____;當四棱錐![]() 的體積取得最大值時,二面角
的體積取得最大值時,二面角![]() 的正切值為_______.
的正切值為_______.
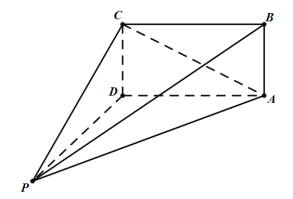
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() 是橢圓上一動點(與左、右頂點不重合)已知
是橢圓上一動點(與左、右頂點不重合)已知![]() 的內切圓半徑的最大值為
的內切圓半徑的最大值為![]() ,橢圓的離心率為
,橢圓的離心率為![]() .
.
(1)求橢圓C的方程;
(2)過![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,過
兩點,過![]() 作
作![]() 軸的垂線交橢圓
軸的垂線交橢圓![]() 與另一點
與另一點![]() (
(![]() 不與
不與![]() 重合).設
重合).設![]() 的外心為
的外心為![]() ,求證
,求證![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究不同性別在處理多任務時的表現差異,召集了男女志愿者各200名,要求他們同時完成多個任務,包括解題、讀地圖、接電話.下圖表示了志愿者完成任務所需的時間分布.以下結論,對志愿者完成任務所需的時間分布圖表理解正確的是( )

①總體看女性處理多任務平均用時更短;
②所有女性處理多任務的能力都要優于男性;
③男性的時間分布更接近正態分布;
④女性處理多任務的用時為正數,男性處理多任務的用時為負數.
A.①④B.②③C.①③D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某少兒游泳隊需對隊員進行限時的仰臥起坐達標測試.已知隊員的測試分數![]() 與仰臥起坐
與仰臥起坐
個數![]() 之間的關系如下:
之間的關系如下: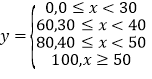 ;測試規則:每位隊員最多進行三組測試,每組限時1分鐘,當一組測完,測試成績達到60分或以上時,就以此組測試成績作為該隊員的成績,無需再進行后續的測試,最多進行三組;根據以往的訓練統計,隊員“喵兒”在一分鐘內限時測試的頻率分布直方圖如下:
;測試規則:每位隊員最多進行三組測試,每組限時1分鐘,當一組測完,測試成績達到60分或以上時,就以此組測試成績作為該隊員的成績,無需再進行后續的測試,最多進行三組;根據以往的訓練統計,隊員“喵兒”在一分鐘內限時測試的頻率分布直方圖如下:
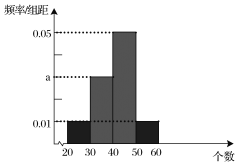
(1)計算![]() 值;
值;
(2)以此樣本的頻率作為概率,求
①在本次達標測試中,“喵兒”得分等于![]() 的概率;
的概率;
②“喵兒”在本次達標測試中可能得分的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com