
【題目】某無縫鋼管廠只生產甲、乙兩種不同規格的鋼管,鋼管有內外兩個口徑,甲種鋼管內外兩口徑的標準長度分別為![]() 和
和![]() ,乙種鋼管內外兩個口徑的標準長度分別為
,乙種鋼管內外兩個口徑的標準長度分別為![]() 和
和![]() .根據長期的生產結果表明,兩種規格鋼管每根的長度
.根據長期的生產結果表明,兩種規格鋼管每根的長度![]() 都服從正態分布
都服從正態分布![]() ,長度在
,長度在![]() 之外的鋼管為廢品,要回爐熔化,不準流入市場,其他長度的鋼管為正品.
之外的鋼管為廢品,要回爐熔化,不準流入市場,其他長度的鋼管為正品.
(1)在該鋼管廠生產的鋼管中隨機抽取10根進行檢測,求至少有1根為廢品的概率;
(2)監管部門規定每種規格鋼管的“口徑誤差”的計算方式為:若鋼管的內外兩個口徑實際長分別為![]() ,標準長分別為
,標準長分別為![]() ,則“口徑誤差”為
,則“口徑誤差”為![]() ,按行業生產標準,其中“一級品”“二級品”“合格品”的“口徑誤差”的范圍分別是
,按行業生產標準,其中“一級品”“二級品”“合格品”的“口徑誤差”的范圍分別是![]() (正品鋼管中沒有“口徑誤差”大于
(正品鋼管中沒有“口徑誤差”大于![]() 的鋼管),現分別從甲、乙兩種產品的正品中各隨機抽取100根,分別進行“口徑誤差”的檢測,統計后,繪制其頻率分布直方圖如圖所示:
的鋼管),現分別從甲、乙兩種產品的正品中各隨機抽取100根,分別進行“口徑誤差”的檢測,統計后,繪制其頻率分布直方圖如圖所示:
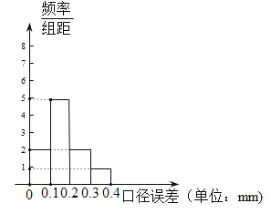

甲種鋼管 乙種鋼管
已知經銷商經銷甲種鋼管,其中“一級品”的利潤率為0.3,“二級品”的利潤率為0.18,“合格品”的利潤率為0.1;經銷乙種鋼管,其中“一級品”的利潤率為0.25,“二級品”的利潤率為0.15,“合格品”的利潤率為0.08,若視頻率為概率.
(ⅰ)若經銷商對甲、乙兩種鋼管各進了100萬元的貨,![]() 和
和![]() 分別表示經銷甲、乙兩種鋼管所獲得的利潤,求
分別表示經銷甲、乙兩種鋼管所獲得的利潤,求![]() 和
和![]() 的數學期望和方差,并由此分析經銷商經銷兩種鋼管的利弊;
的數學期望和方差,并由此分析經銷商經銷兩種鋼管的利弊;
(ⅱ)若經銷商計劃對甲、乙兩種鋼管總共進100萬元的貨,則分別在甲、乙兩種鋼管上進貨多少萬元時,可使得所獲利潤的方差和最小?
附:若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() .
.
【答案】(1)![]() ;(2)(ⅰ)
;(2)(ⅰ)![]() ,
,![]() ,
,![]() ,利弊見解析;(ⅱ)甲種鋼管上投資25萬元,在乙種鋼管上投資75萬元
,利弊見解析;(ⅱ)甲種鋼管上投資25萬元,在乙種鋼管上投資75萬元
【解析】
(1)結合題意,由正態分布的概率進行計算即可;
(2)(ⅰ)根據題意,求解分布列,再根據分布列求解期望和方差即可;
(ⅱ)構造方差和的函數,根據方差的運算性質,利用已知求函數的最小值即可.
(1)由正態分布可知,抽取的1根鋼管的長度在![]() 之內的概率為0.9974,
之內的概率為0.9974,
則這10根鋼管的長度全在![]() 內的概率為
內的概率為![]() ,
,
則這10根中至少有1根為廢品的概率約為![]() .
.
(2)(ⅰ)由利潤率和投額可得![]() 可為30萬元、18萬元、10萬元,
可為30萬元、18萬元、10萬元,
![]() 可為25萬元、15萬元、8萬元.
可為25萬元、15萬元、8萬元.
又由直方圖可得對應的頻率為0.2、0.5、0.3和0.2、0.8、0,
所以隨機變量![]() 的分布列為
的分布列為
| 30 | 18 | 10 |
| 0.2 | 0.5 | 0.3 |
![]() (萬元),
(萬元),
![]() .
.
隨機變量![]() 的分布列為
的分布列為
| 25 | 15 | 8 |
| 0.2 | 0.8 | 0 |
![]() (萬元),
(萬元),![]() .
.
經銷商經銷甲種鋼管的平均利潤18萬元大于經銷乙種鋼管的平均利潤17萬元,
但經銷甲種鋼管的方差48大于經銷乙種鋼管的方差16.
所以經銷甲種鋼管的平均利潤大,方差也大,相對不穩定;
而經銷乙種鋼管的平均利潤小,方差也小,相對穩定.
(ⅱ)設經銷商進了![]() 萬元的甲種鋼管,則進了
萬元的甲種鋼管,則進了![]() 萬元的乙種鋼管,
萬元的乙種鋼管,
令![]() 為經銷甲種鋼管所獲利潤的方差與經銷乙種鋼管所獲利潤的方差的和,則
為經銷甲種鋼管所獲利潤的方差與經銷乙種鋼管所獲利潤的方差的和,則
![]()
![]()
![]()
![]() .
.
當![]() 時,
時,![]() 的值最小.
的值最小.
故在甲種鋼管上投資25萬元,在乙種鋼管上投資75萬元時,
可使經銷甲種鋼管所獲利潤的方差與經銷乙種鋼管所獲利潤的方差和最小.


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:高中數學 來源: 題型:
【題目】在某公司舉行的年終慶典活動中,主持人利用隨機抽獎軟件進行抽獎:由電腦隨機生成一張如圖所示的3![]() 3表格,其中1格設獎300元,4格各設獎200元,其余4格各設獎100元,點擊某一格即顯示相應金額.某人在一張表中隨機不重復地點擊3格,記中獎的總金額為X元.
3表格,其中1格設獎300元,4格各設獎200元,其余4格各設獎100元,點擊某一格即顯示相應金額.某人在一張表中隨機不重復地點擊3格,記中獎的總金額為X元.
(1)求概率![]() ;
;
(2)求![]() 的概率分布及數學期望
的概率分布及數學期望![]() .
.

查看答案和解析>>
科目:高中數學 來源: 題型:
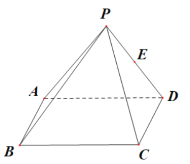
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形,![]() ,側面
,側面![]() 為等邊三角形且垂直于底面
為等邊三角形且垂直于底面![]() ,
,![]() 是
是![]() 的中點.
的中點.
(1)在棱![]() 上取一點
上取一點![]() 使直線
使直線![]() ∥平面
∥平面![]() 并證明;
并證明;
(2)在(1)的條件下,當棱![]() 上存在一點
上存在一點![]() ,使得直線
,使得直線![]() 與底面
與底面![]() 所成角為
所成角為![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓O:x2+y2=3上的一動點M在x軸上的投影為N,點P滿足![]() .
.
(1)求動點P的軌跡C的方程;
(2)若直線l與圓O相切,且交曲線C于點A,B,試求|AB|的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某學校高三年級共1000名男生中隨機抽取50人測量身高,據測量,被測學生身高全部介于![]() 到
到![]() 之間,將測量結果按如下方式分成八組:第一組
之間,將測量結果按如下方式分成八組:第一組![]() ,第二組
,第二組![]() ,…,第八組
,…,第八組![]() .如圖是按上述分組方法得到的頻率分布直方圖的一部分.其中第六組、第七組、第八組人數依次構成等差數列.
.如圖是按上述分組方法得到的頻率分布直方圖的一部分.其中第六組、第七組、第八組人數依次構成等差數列.
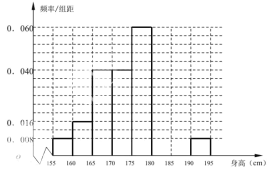
(1)求第六組、第七組的頻率,并估計高三年級全體男生身高在![]() 以上(含
以上(含![]() )的人數;
)的人數;
(2)學校決定讓這五十人在運動會上組成一個高旗隊,在這五十人中要選身高在![]() 以上(含
以上(含![]() )的兩人作為隊長,求這兩人在同一組的概率.
)的兩人作為隊長,求這兩人在同一組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某景區內有一半圓形花圃,其直徑AB為6,O是圓心,且OC⊥AB.在OC上有一座觀賞亭Q,其中∠AQC=![]() ,.計劃在
,.計劃在![]() 上再建一座觀賞亭P,記∠POB=θ
上再建一座觀賞亭P,記∠POB=θ![]() .
.
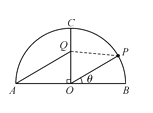
(1)當θ=![]() 時,求∠OPQ的大小;
時,求∠OPQ的大小;
(2)當∠OPQ越大時,游客在觀賞亭P處的觀賞效果越佳,求游客在觀賞亭P處的觀賞效果最佳時,角θ的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公園內有一塊以![]() 為圓心半徑為
為圓心半徑為![]() 米的圓形區域.為豐富市民的業余文化生活,現提出如下設計方案:如圖,在圓形區域內搭建露天舞臺,舞臺為扇形
米的圓形區域.為豐富市民的業余文化生活,現提出如下設計方案:如圖,在圓形區域內搭建露天舞臺,舞臺為扇形![]() 區域,其中兩個端點
區域,其中兩個端點![]() ,
,![]() 分別在圓周上;觀眾席為梯形
分別在圓周上;觀眾席為梯形![]() 內切在圓
內切在圓![]() 外的區域,其中
外的區域,其中![]() ,
,![]() ,且
,且![]() ,
,![]() 在點
在點![]() 的同側.為保證視聽效果,要求觀眾席內每一個觀眾到舞臺
的同側.為保證視聽效果,要求觀眾席內每一個觀眾到舞臺![]() 處的距離都不超過
處的距離都不超過![]() 米.設
米.設![]() ,
,![]() .問:對于任意
.問:對于任意![]() ,上述設計方案是否均能符合要求?
,上述設計方案是否均能符合要求?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,a,b,c分別是角A,B,C的對邊,且acosC=(2b﹣c)cosA.
(1)若![]() 3,求△ABC的面積;
3,求△ABC的面積;
(2)若∠B<∠C,求2cos2B+cos2C的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com