
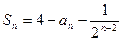 .(Ⅰ)求
.(Ⅰ)求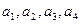 ;
;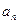 的表達式,并用數學歸納法加以證明.
的表達式,并用數學歸納法加以證明. 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案 學習實踐園地系列答案
學習實踐園地系列答案科目:高中數學 來源:不詳 題型:解答題
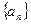 中,
中,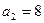 ,前
,前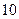 項和
項和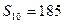
 .
. 通項
通項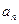 ;
;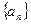 中依次取第
中依次取第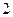 項、第
項、第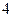 項、第
項、第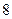 項…第
項…第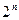 項……按原來的順序組成一個新的數列
項……按原來的順序組成一個新的數列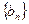 ,求數列
,求數列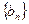 的前n項和
的前n項和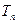 .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com