已知向量
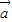
、
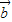
的夾角為60°,且|
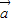
|=2,|
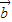
|=1,則向量
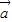
與向量
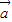
+2
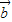
的夾角等于( )
A.150°
B.90°
C.60°
D.30°
【答案】
分析:先求出
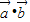
及|
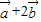
|=
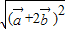
=
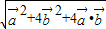
的值,再根據(jù)cosθ=
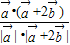
求出θ 的值.
解答:解:由題意可得
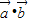
=2×1cos60°=1,設(shè)向量
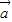
與向量
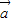
+2
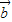
的夾角等于θ,
則|

|=

=
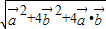
=2
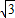
.
故cosθ=
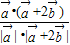
=
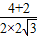
=
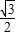
.
再由 0°≤θ≤180°,可得θ=30°,
故選D.
點(diǎn)評(píng):本題主要考查兩個(gè)向量的夾角公式,兩個(gè)向量數(shù)量積公式,求向量的模的方法,屬于中檔題.
練習(xí)冊(cè)系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:
題型:
已知向量
,的夾角為
,且
||=,
||=2,在△ABC中,
=+,=-3,D為BC邊的中點(diǎn),則
||=( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
已知向量
•的夾角為
,且
||=,||=2,|-|=( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
在△ABC中,a、b、c分別為角A、B、C的對(duì)邊,已知向量
=(sinB,1-cosB)與向量
=(0,1) 的夾角為
,
求:(I) 角B 的大小; (Ⅱ)
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
(2011•孝感模擬)已知橢圓C:
+=1(a>b>0)的左右焦點(diǎn)分別為F
1、F
2,P是橢圓上一點(diǎn),向量
與向量
的夾角為
,且
在
上的投影的大小恰為|
|,則橢圓的離心率為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:2011-2012學(xué)年湖北省黃岡市蘄春縣李時(shí)珍中學(xué)高三(上)第三次月考數(shù)學(xué)試卷(文科)(解析版)
題型:填空題
已知向量

,

的夾角為

,且|

|=

,|

|=2.在△ABC中,

=2

+2

,

=2

-6

,D為BC邊的中點(diǎn),則|

|=
.
查看答案和解析>>

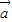 、
、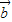 的夾角為60°,且|
的夾角為60°,且|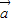 |=2,|
|=2,|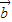 |=1,則向量
|=1,則向量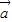 與向量
與向量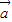 +2
+2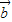 的夾角等于( )
的夾角等于( )
 ,
, 的夾角為
的夾角為 ,且|
,且| |=
|= ,|
,| |=2.在△ABC中,
|=2.在△ABC中, =2
=2 +2
+2 ,
, =2
=2 -6
-6 ,D為BC邊的中點(diǎn),則|
,D為BC邊的中點(diǎn),則| |= .
|= .