
某校高一年級60名學生參加數學競賽,成績全部在40分至100分之間,現將成績分成以下6段: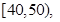
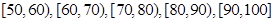 ,據此繪制了如圖所示的頻率分布直方圖.
,據此繪制了如圖所示的頻率分布直方圖. 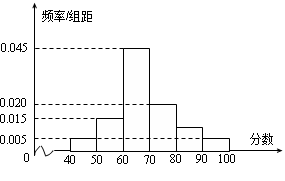
(1)求成績在區間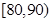 的頻率;
的頻率;
(2)從成績大于等于80分的學生中隨機選3名學生,其中成績在[90,100]內的學生人數為ξ,求ξ的分布列與均值.
(1) ;(2)分布列詳見解析,
;(2)分布列詳見解析,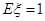 .
.
解析試題分析:本題主要考查頻率分步直方圖和離散型隨機變量的分布列和數學期望等數學知識,考查學生的讀圖能力、分析問題和解決問題的能力、計算能力.第一問,利用頻率分布直方圖可知,所有頻率之和為1,所有可以求出成績在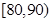 的頻率;第二問,通過頻率分布直方圖分別求出
的頻率;第二問,通過頻率分布直方圖分別求出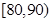 和
和 內的學生人數,先列出
內的學生人數,先列出 的可能取值,再分別求出每一種情況下的概率列出分布列,利用
的可能取值,再分別求出每一種情況下的概率列出分布列,利用 求數學期望.
求數學期望.
試題解析:(1)因為各組的頻率之和為1,所以成績在區間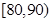 的頻率為
的頻率為 , 3分
, 3分
(2)由已知和(1)的結果可知成績在區間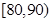 內的學生有
內的學生有 人,
人,
成績在區間 內的學生有
內的學生有 人, 4 分
人, 4 分
依題意,ξ可能取的值為0,1,2,3 5 分
所以ξ的分布列為ξ 0 1 2 3 P 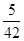



10分
則均值Eξ= 12分
12分
考點:1.頻率分布直方圖;2.離散型隨機變量的分布列和數學期望.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:高中數學 來源: 題型:解答題
某種產品的廣告費支出x與銷售額 (單位:百萬元)之間有如下對應數據:
(單位:百萬元)之間有如下對應數據:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
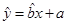 .
. ,你可得到什么結論?
,你可得到什么結論?查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某種水果的單個質量在500g以上視為特等品.隨機抽取1000個該水果,結果有50個特等品.將這50個水果的質量數據分組,得到下邊的頻率分布表.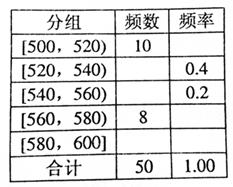
(1)估計該水果的質量不少于560g的概率;
(2)若在某批水果的檢測中,發現有15個特等品,據此估計該批水果中沒有達到特等品的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某市為“市中學生知識競賽”進行選拔性測試,且規定:成績大于或等于90分的有參賽資格,90分以下(不包括90分)的被淘汰.若有500人參加測試,學生成績的頻率分布直方圖如圖.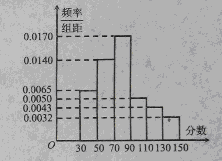
(1)求獲得參賽資格的人數;
(2)根據頻率直方圖,估算這500名學生測試的平均成績;
(3)若知識競賽分初賽和復賽,在初賽中每人最多有5次選題答題的機會,累計答對3題或答錯3題即終止,答對3題者方可參加復賽.已知參賽者甲答對每一個問題的概率都相同,并且相互之間沒有影響.已知他連續兩次答錯的概率為 ,求甲在初賽中答題個數
,求甲在初賽中答題個數 的分布列及數學期望
的分布列及數學期望 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一個車間為了規定工時定額.需要確定加工零件所花費的時間,為此進行了10次試驗.測得的數據如下:
| 零件數x/個 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 加工時間y/分 | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某地區有小學21所,中學14所,大學7所,現采用分層抽樣的方法從這些學校中抽取6所學校對學生進行視力調查.
(1)求應從小學、中學、大學中分別抽取的學校數目;
(2)若從抽取的6所學校中隨機抽取2所學校做進一步數據分析,
①列出所有可能的抽取結果;
②求抽取的2所學校均為小學的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某班主任對全班50名學生學習積極性和對待班級工作的態度進行了調查,統計數據如下表所示:
| | 積極參加班級工作 | 不太主動參加班級工作 | 合計 |
| 學習積極性高 | 18 | 7 | 25 |
| 學習積極性一般 | 6 | 19 | 25 |
| 合計 | 24 | 26 | 50 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某單位N名員工參加“社區低碳你我他”活動,他們的年齡在25歲至50歲之間。按年齡分組:第1組 ,第2組
,第2組 ,第3組
,第3組 ,第4組
,第4組 ,第5組
,第5組 ,由統計的數據得到的頻率分布直方圖如圖所示,下表是年齡的頻率分布表。
,由統計的數據得到的頻率分布直方圖如圖所示,下表是年齡的頻率分布表。
| 區間 |  |  |  |  |  |
| 人數 |  | a | b | | |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某車間共有12名工人,隨機抽取6名,他們某日加工零件個數的莖葉圖如圖所示,其中莖為十位數,葉為個位數.
(1)根據莖葉圖計算樣本均值.
(2)日加工零件個數大于樣本均值的工人為優秀工人.根據莖葉圖推斷該車間12名工人中有幾名優秀工人?
(3)從該車間12名工人中,任取2人,求恰有1名優秀工人的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com