
某單位N名員工參加“社區低碳你我他”活動,他們的年齡在25歲至50歲之間。按年齡分組:第1組 ,第2組
,第2組 ,第3組
,第3組 ,第4組
,第4組 ,第5組
,第5組 ,由統計的數據得到的頻率分布直方圖如圖所示,下表是年齡的頻率分布表。
,由統計的數據得到的頻率分布直方圖如圖所示,下表是年齡的頻率分布表。
| 區間 |  |  |  |  |  |
| 人數 |  | a | b | | |
(1)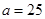 人,
人,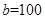 人,
人,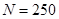 人;(2)第1,2,3組分別抽取1人,1人,4人;
人;(2)第1,2,3組分別抽取1人,1人,4人;
(3)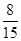
解析試題分析:(1)利用頻率分布直方圖即可求出;(2)抓住分層抽樣的抽樣比為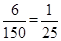 即可解決問題;
即可解決問題;
(3)列出從6個人抽取2人的所以情況,然后從中找到滿足條件的情況是多少個,最后利用古典概型公式即可.
試題解析:(1)由頻率分布直方圖可知, 與
與 兩組的人數相同,
兩組的人數相同,
所以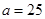 人. 1分
人. 1分
且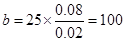 人. 2分
人. 2分
總人數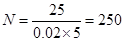 人. 3分
人. 3分
(2)因為第1,2,3組共有25+25+100=150人,利用分層抽樣在150名員工中抽取 人,每組抽取的人數分別為:
人,每組抽取的人數分別為:
第1組的人數為 , 4分
, 4分
第2組的人數為 , 5分
, 5分
第3組的人數為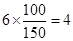 , 6分
, 6分
所以第1,2,3組分別抽取1人,1人,4人.7分
(3)由(2)可設第1組的1人為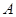 ,第2組的1人為
,第2組的1人為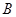 ,第3組的4人分別為
,第3組的4人分別為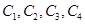 ,則從6人中抽取2人的所有可能結果為:
,則從6人中抽取2人的所有可能結果為: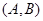 ,
,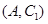 ,
,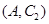 ,
,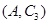 ,
,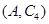 ,
,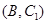 ,
,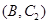 ,
,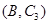 ,
,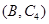 ,
,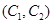 ,
,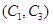 ,
,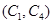 ,
,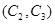 ,
,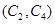 ,
,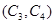 ,
,
共有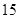 種. 9分
種. 9分
其中恰有1人年齡在第3組的所有結果為: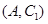 ,
,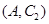 ,
,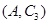 ,
,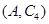 ,
,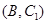 ,
,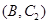 ,
,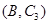 ,
,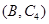 ,
,
共有8種. 2分
所以恰有1人年齡在第3組的概率為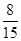 .12分
.12分
考點:(1)頻率分布直方圖;(2)分層抽樣;(3)古典概型.


 活力試卷系列答案
活力試卷系列答案 課課優能力培優100分系列答案
課課優能力培優100分系列答案科目:高中數學 來源: 題型:解答題
某公司生產產品A,產品質量按測試指標分為:指標大于或等于90為一等品,大于或等于 小于
小于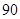 為二等品,小于
為二等品,小于 為三等品,生產一件一等品可盈利50元,生產一件二等品可盈利
為三等品,生產一件一等品可盈利50元,生產一件二等品可盈利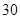 元,生產一件三等品虧損10元.現隨機抽查熟練工人甲和新工人乙生產的這種產品各100件進行檢測,檢測結果統計如下:
元,生產一件三等品虧損10元.現隨機抽查熟練工人甲和新工人乙生產的這種產品各100件進行檢測,檢測結果統計如下:
| 測試指標 | 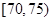 | 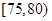 | 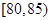 | 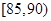 | 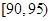 | 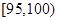 |
| 甲 | 3 | 7 | 20 | 40 | 20 | 10 |
| 乙 | 5 | 15 | 35 | 35 | 7 | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校高一年級60名學生參加數學競賽,成績全部在40分至100分之間,現將成績分成以下6段: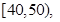
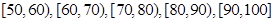 ,據此繪制了如圖所示的頻率分布直方圖.
,據此繪制了如圖所示的頻率分布直方圖. 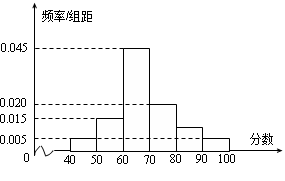
(1)求成績在區間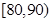 的頻率;
的頻率;
(2)從成績大于等于80分的學生中隨機選3名學生,其中成績在[90,100]內的學生人數為ξ,求ξ的分布列與均值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
隨機抽取某中學高一級學生的一次數學統測成績得到一樣本,其分組區間和頻數是: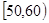 ,2;
,2;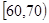 ,7;
,7;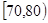 ,10;
,10;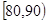 ,x;[90,100],2.其頻率分布直方圖受到破壞,可見部分如下圖所示,據此解答如下問題.
,x;[90,100],2.其頻率分布直方圖受到破壞,可見部分如下圖所示,據此解答如下問題.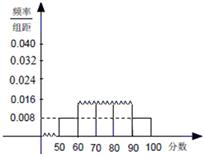
(1)求樣本的人數及x的值;
(2)估計樣本的眾數,并計算頻率分布直方圖中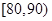 的矩形的高;
的矩形的高;
(3)從成績不低于80分的樣本中隨機選取2人,該2人中成績在90分以上(含90分)的人數記為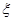 ,求
,求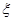 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對某電子元件進行壽命追蹤調查,所得樣本數據的頻率分布直方圖如下.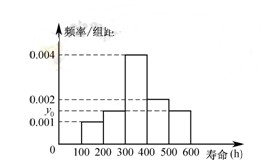
(1)求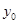 ,并根據圖中的數據,用分層抽樣的方法抽取
,并根據圖中的數據,用分層抽樣的方法抽取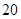 個元件,元件壽命落在
個元件,元件壽命落在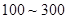 之間的應抽取幾個?
之間的應抽取幾個?
(2)從(1)中抽出的壽命落在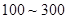 之間的元件中任取
之間的元件中任取 個元件,求事件“恰好有一個元件壽命落在
個元件,求事件“恰好有一個元件壽命落在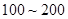 之間,一個元件壽命落在
之間,一個元件壽命落在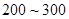 之間”的概率.
之間”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了比較兩種治療失眠癥的藥(分別稱為A藥,B藥)的療效,隨機地選取20位患者服用A藥,20位患者服用B藥,這40位患者在服用一段時間后,記錄他們日平均增加的睡眠時間(單位:h).試驗的觀測結果如下:
服用A藥的20位患者日平均增加的睡眠時間:
| 0.6 | 1.2 | 2.7 | 1.5 | 2.8 | 1.8 | 2.2 | 2.3 | 3.2 | 3.5 |
| 2.5 | 2.6 | 1.2 | 2.7 | 1.5 | 2.9 | 3.0 | 3.1 | 2.3 | 2.4 |
| 3.2 | 1.7 | 1.9 | 0.8 | 0.9 | 2.4 | 1.2 | 2.6 | 1.3 | 1.4 |
| 1.6 | 0.5 | 1.8 | 0.6 | 2.1 | 1.1 | 2.5 | 1.2 | 2.7 | 0.5 |
| A藥 | | B藥 |
| | 0. 1. 2. 3. | |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
農科院的專家為了了解新培育的甲、乙兩種麥苗的長勢情況,從甲、乙兩種麥苗的試驗田中各抽取6株麥苗測量麥苗的株高,數據如下:(單位: )
)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在上面給出的方框內繪出所抽取的甲、乙兩種麥苗株高的莖葉圖;
(2)分別計算所抽取的甲、乙兩種麥苗株高的平均數與方差,并由此判斷甲、乙兩種麥苗的長勢情況.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了解高二某班學生喜愛打籃球是否與性別有關,對本班50人進行了問卷調查得到了如下的列聯表:
已知在全部50人中隨機抽取1人抽到喜愛打籃球的學生的概率為 .
.
(1)請將上面的列聯表補充完整;
(2)是否有99.5%的把握認為喜愛打籃球與性別有關?說明你的理由;
下面的臨界值表供參考:
(參考公式K2=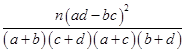 ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
經銷商經銷某種農產品,在一個銷售季度內,每售出 t該產品獲利潤
t該產品獲利潤 元,未售出的產品,每
元,未售出的產品,每 t虧損
t虧損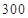 元。根據歷史資料,得到銷售季度內市場需求量的頻率分布直方圖,如圖所示。經銷商為下一個銷售季度購進了
元。根據歷史資料,得到銷售季度內市場需求量的頻率分布直方圖,如圖所示。經銷商為下一個銷售季度購進了 t該農產品,以
t該農產品,以 (單位:t,
(單位:t,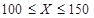 )表示下一個銷售季度內的市場需求量,
)表示下一個銷售季度內的市場需求量,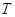 (單位:元)表示下一個銷售季度內銷商該農產品的利潤。
(單位:元)表示下一個銷售季度內銷商該農產品的利潤。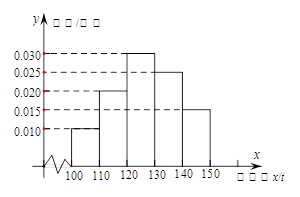
(1)將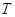 表示為
表示為 的函數;
的函數;
(2)根據直方圖估計利潤 不少于57000元的概率;
不少于57000元的概率;
(3)在直方圖的需求量分組中,以各組的區間中點值代表該組的各個值,并以需求量落入該區間的頻率作為需求量取該區間中點值的概率(例如:若 ,則取
,則取 ,且
,且 的概率等于需求量落入
的概率等于需求量落入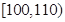 的概率),求利潤
的概率),求利潤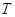 的數學期望.
的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com